1. 多元函数的基本概念
1. 二元函数的概念
设有变量 \(x\text{ 、 }y\) 和 \(z\) ,如果变量 \(x\text{ 、 }y\) 在一定范围内取定一组值时,变量 \(z\) 按照一定的法则,总有唯一确定的数值与之对应,则称 \(z\) 是 \(x\text{ 、 }y\) 的二元函数,记为\[z = f\left( {x,y}\right)\]并称 \(x\text{ 、 }y\) 为自变量.
自变量 \(x\text{ 、 }y\) 的取值范围,叫做函数的定义域.
在空间直角坐标系中,二元函数 \(z = f\left( {x,y}\right)\) 的图形通常是一张曲面,它的定义域是这张曲面在 \({xOy}\) 平面上的投影.
类似地, 可以定义三元以及三元以上的函数. 二元及二元以上的函数, 统称多元函数.
2. 二元函数的极限
设二元函数 \(z = f\left( {x,y}\right)\) 定义在平面点集 \(E\) 上, \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 是 \(E\) 的聚点, \(A\) 为一常数. 若对于任意给定的正数 \(\varepsilon\) ,总存在正数 \(\delta\) ,使得适合不等式 \(0 < \left| {{P}_{0}P}\right| = \sqrt{{\left( x - {x}_{0}\right) }^{2} + {\left( y - {y}_{0}\right) }^{2}} < \delta\) 的一切点 \(P\left( {x,y}\right)\) 都有\[\left| {f\left( {x,y}\right) - A}\right| < \varepsilon\]成立,则称 \(A\) 为函数 \(z = f\left( {x,y}\right)\) 当 \(x \rightarrow {x}_{0},y \rightarrow {y}_{0}\) 时的极限,记为 \(\mathop{\lim }\limits_{\substack{{x \rightarrow {x}_{0}} \\ {y \rightarrow {y}_{0}} }}f\left( {x,y}\right) = A\) . 这时也称当 \(x \rightarrow {x}_{0},y \rightarrow {y}_{0}\) 时,函数 \(f\left( {x,y}\right)\) 收敛于 \(A\) .
为了区别于一元函数极限, 把上述二元函数的极限叫做二重极限.
所谓二重极限存在,是指点 \(P\left( {x,y}\right)\) 以任何方式无限趋于点 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 时,函数 \(f\left( {x,y}\right)\) 都趋于同一数值 \(A\) . 因此,如果点 \(P\left( {x,y}\right)\) 以某一特殊方式,例如沿某一定直线或定曲线趋近于 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 时,即使函数趋于某一确定值,也不能由此断定函数的极限存在. 但是反过来,如果当 \(P\left( {x,y}\right)\) 以不同方式趋于 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 时,函数趋于不同的值,那么就可以断定该函数的极限不存在.
3. 二元函数的连续性
设函数 \(z = f\left( {x,y}\right)\) 的定义域为 \(D,{P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 是 \(D\) 的聚点,且 \({P}_{0} \in D\) ,若\[\mathop{\lim }\limits_{\substack{{x \rightarrow {x}_{0}} \\ {y \rightarrow {y}_{0}} }}f\left( {x,y}\right) = f\left( {{x}_{0},{y}_{0}}\right)\]则称函数 \(z = f\left( {x,y}\right)\) 在点 \({P}_{0}\) 处连续.
若函数在区域 \(D\) 内的每一点都连续,则称函数 \(f\left( {x,y}\right)\) 在区域 \(D\) 内连续.
多元初等函数在其定义域内是连续函数.
4. 有界闭区域上二元连续函数的性质
最大值和最小值定理 在有界闭区域上的二元连续函数, 在该区域上至少取得它的最大值和最小值各一次.
介值定理 在有界闭区域上的二元连续函数, 如果取得两个不同的函数值, 则函数在该区域上必取得介于这两个值之间的任何值.
特别地,若 \(\mu\) 是介于在有界闭区域上连续的函数 \(f\left( {x,y}\right)\) 的最小值 \(m\) 和最大值 \(M\) 之间的一个数,则在该区域中至少存在一点 \(P\left( {\xi ,\eta }\right)\) ,使得 \(f\left( {\xi ,\eta }\right) = \mu\).
2. 偏导数
1. 偏导数的定义\[\frac{\partial z}{\partial x} = \mathop{\lim }\limits_{{{\Delta x} \rightarrow 0}}\frac{f\left( {x + {\Delta x},y}\right) - f\left( {x,y}\right) }{\Delta x}\]\[\frac{\partial z}{\partial y} = \mathop{\lim }\limits_{{{\Delta y} \rightarrow 0}}\frac{f\left( {x,y + {\Delta y}}\right) - f\left( {x,y}\right) }{\Delta y}\]
2. 高阶偏导数
函数 \(z = f\left( {x,y}\right)\) 在区域 \(D\) 内的偏导数 \({f}_{x}^{\prime }\left( {x,y}\right) ,{f}_{y}^{\prime }\left( {x,y}\right)\) 存在时,仍然是 \(x,y\) 的二元函数. 若这两个函数的偏导数\[\frac{\partial }{\partial x}\left( \frac{\partial z}{\partial x}\right) = \frac{{\partial }^{2}z}{\partial {x}^{2}} = {f}_{xx}^{\prime \prime }\left( {x,y}\right)\]\[\frac{\partial }{\partial y}\left( \frac{\partial z}{\partial x}\right) = \frac{{\partial }^{2}z}{\partial x\partial y} = {f}_{xy}^{\prime \prime }\left( {x,y}\right)\]\[\frac{\partial }{\partial x}\left( \frac{\partial z}{\partial y}\right) = \frac{{\partial }^{2}z}{\partial y\partial x} = {f}_{yx}^{\prime \prime }\left( {x,y}\right)\]\[\frac{\partial }{\partial y}\left( \frac{\partial z}{\partial y}\right) = \frac{{\partial }^{2}z}{\partial {y}^{2}} = {f}_{yy}^{\prime \prime }\left( {x,y}\right)\]也存在,则称它们是函数 \(z = f\left( {x,y}\right)\) 的二阶偏导数.
二阶偏导数 \(\frac{{\partial }^{2}z}{\partial x\partial y}\) 与 \(\frac{{\partial }^{2}z}{\partial y\partial x}\) 称为函数 \(z = f\left( {x,y}\right)\) 的二阶混合偏导数. 当这两个二阶混合偏导数在区域 \(D\) 内连续时,则在该区域 \(D\) 内有\[\frac{{\partial }^{2}z}{\partial x\partial y} = \frac{{\partial }^{2}z}{\partial y\partial x}\]
3. 全微分
1. 全微分的定义
设 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 为 \(f\) 定义域 \(D\) 的一个内点,如果函数 \(z = f\left( {x,y}\right)\) 在点 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 处的全增量 \({\Delta z}\) 可表示为\[{\Delta z} = f\left( {{x}_{0} + {\Delta x},{y}_{0} + {\Delta y}}\right) - f\left( {{x}_{0},{y}_{0}}\right) = A \cdot {\Delta x} + B \cdot {\Delta y} + o\left( \rho \right)\]其中 \(A,B\) 是与 \({\Delta x},{\Delta y}\) 无关的常数. 则称函数 \(z = f\left( {x,y}\right)\) 在点 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 处可微,并称函数 \(z =\) \(f\left( {x,y}\right)\) 的全增量 \({\Delta z}\) 的线性主部 \(A \cdot {\Delta x} + B \cdot {\Delta y}\) 为函数 \(z = f\left( {x,y}\right)\) 在点 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 处的全微分, 记作\[\mathrm{d}z = A \cdot {\Delta x} + B \cdot {\Delta y} = A\mathrm{\;d}x + B\mathrm{\;d}y\;\left( {\mathrm{\;d}x = {\Delta x},\mathrm{\;d}y = {\Delta y}}\right)\]当函数 \(z = f\left( {x,y}\right)\) 在点 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 处可微时有\[\mathrm{d}z = {f}_{x}^{\prime }\left( {{x}_{0},{y}_{0}}\right) \mathrm{d}x + {f}_{y}^{\prime }\left( {{x}_{0},{y}_{0}}\right) \mathrm{d}y\]2. 全微分的形式不变性
设 \(z = f\left( {u,v}\right)\) 具有连续偏导数, \(u = \varphi \left( {x,y}\right) ,v = \psi \left( {x,y}\right)\) 也具有连续偏导数,则复合函数 \(z =\) \(f\left\lbrack {\varphi \left( {x,y}\right) ,\psi \left( {x,y}\right) }\right\rbrack\) 在点(x, y)处的全微分为\[\mathrm{d}z = \frac{\partial z}{\partial u}\mathrm{\;d}u + \frac{\partial z}{\partial v}\mathrm{\;d}v\]
4. 多元复合函数的求导法则
1. 复合函数的偏导数
设函数 \(u = \varphi \left( {x,y}\right) ,v = \psi \left( {x,y}\right)\) 在点(x, y)处存在偏导数,又函数 \(z = f\left( {u,v}\right)\) 在对应点(u, v) 处具有连续的一阶偏导数,则复合函数 \(z = f\left\lbrack {\varphi \left( {x,y}\right) ,\psi \left( {x,y}\right) }\right\rbrack\) 在点(x, y)处对 \(x\) 及 \(y\) 的偏导数均存在, 且有\[\frac{\partial z}{\partial x} = \frac{\partial z}{\partial u} \cdot \frac{\partial u}{\partial x} + \frac{\partial z}{\partial v} \cdot \frac{\partial v}{\partial x},\;\frac{\partial z}{\partial y} = \frac{\partial z}{\partial u} \cdot \frac{\partial u}{\partial y} + \frac{\partial z}{\partial v} \cdot \frac{\partial v}{\partial y}\]2. 全导数
设函数 \(z = f\left( {u,v}\right)\) ,而 \(u = \varphi \left( x\right) ,v = \psi \left( x\right)\) ,则 \(z = f\left\lbrack {\varphi \left( x\right) ,\psi \left( x\right) }\right\rbrack\) 是 \(x\) 的一元函数,且\[\frac{\mathrm{d}z}{\mathrm{\;d}x} = \frac{\partial z}{\partial u} \cdot \frac{\mathrm{d}u}{\mathrm{\;d}x} + \frac{\partial z}{\partial v} \cdot \frac{\mathrm{d}v}{\mathrm{\;d}x}\]称 \(\frac{\mathrm{d}z}{\mathrm{\;d}x}\) 为 \(z\) 关于 \(x\) 的全导数.
5. 隐函数的求导法则
1. 一元隐函数求导法则
设函数 \(F\left( {x,y}\right)\) 在点 \(P\left( {{x}_{0},{y}_{0}}\right)\) 的某个邻域内具有连续的偏导数 \({F}_{x}^{\prime }\left( {x,y}\right) ,{F}_{y}^{\prime }\left( {x,y}\right)\) ,且 \(F\left( {{x}_{0},{y}_{0}}\right) = 0,{F}_{y}^{\prime }\left( {{x}_{0},{y}_{0}}\right) \neq 0\) ,则在 \(\left( {{x}_{0},{y}_{0}}\right)\) 的某邻域内,方程 \(F\left( {x,y}\right) = 0\) 恒能唯一确定一个具有连续导数的函数 \(y = f\left( x\right)\) ,它满足条件 \({y}_{0} = f\left( {x}_{0}\right)\) ,并有\[\frac{\mathrm{d}y}{\mathrm{\;d}x} = - \frac{{F}_{x}^{\prime }\left( {x,y}\right) }{{F}_{y}^{\prime }\left( {x,y}\right) }\]2. 二元隐函数求导法则
设函数 \(F\left( {x,y,z}\right)\) 在点 \(P\left( {{x}_{0},{y}_{0},{z}_{0}}\right)\) 的某个邻域内具有连续的偏导数 \({F}_{x}^{\prime }\left( {x,y,z}\right)\) , \({F}_{y}^{\prime }\left( {x,y,z}\right) ,{F}_{z}^{\prime }\left( {x,y,z}\right)\) ,且 \(F\left( {{x}_{0},{y}_{0},{z}_{0}}\right) = 0,{F}_{z}^{\prime }\left( {{x}_{0},{y}_{0},{z}_{0}}\right) \neq 0\) ,则在点 \(\left( {{x}_{0},{y}_{0},{z}_{0}}\right)\) 的某一邻域内,方程 \(F\left( {x,y,z}\right) = 0\) 恒能唯一确定一个具有连续偏导数的函数 \(z = f\left( {x,y}\right)\) ,它满足条件 \({z}_{0} =\) \(f\left( {{x}_{0},{y}_{0}}\right)\) ,并有\[\frac{\partial z}{\partial x} = - \frac{{F}_{x}^{\prime }\left( {x,y,z}\right) }{{F}_{z}^{\prime }\left( {x,y,z}\right) }\;,\;\frac{\partial z}{\partial y} = - \frac{{F}_{y}^{\prime }\left( {x,y,z}\right) }{{F}_{z}^{\prime }\left( {x,y,z}\right) }\]
6. 多元函数微分学的几何应用
1. 空间曲线的切线与法平面
设空间曲线的参数方程为 \(\left\{ \begin{array}{l} x = x\left( t\right) \\ y = y\left( t\right) \\ z = z\left( t\right) \end{array}\right.\)
其中 \(x = x\left( t\right) ,y = y\left( t\right) ,z = z\left( t\right)\) 均为 \(t\) 的可微函数,且 \({x}^{\prime }\left( t\right) \text{ 、 }{y}^{\prime }\left( t\right) \text{ 、 }{z}^{\prime }\left( t\right)\) 不同时为零,则当 \(t = {t}_{0}\) 时,曲线上对应点 \({M}_{0}\left( {{x}_{0},{y}_{0},{z}_{0}}\right)\) 处的切线方程为\[\frac{x - {x}_{0}}{{x}^{\prime }\left( {t}_{0}\right) } = \frac{y - {y}_{0}}{{y}^{\prime }\left( {t}_{0}\right) } = \frac{z - {z}_{0}}{{z}^{\prime }\left( {t}_{0}\right) }\]法平面方程为\[{x}^{\prime }\left( {t}_{0}\right) \left( {x - {x}_{0}}\right) + {y}^{\prime }\left( {t}_{0}\right) \left( {y - {y}_{0}}\right) + {z}^{\prime }\left( {t}_{0}\right) \left( {z - {z}_{0}}\right) = 0\]2. 曲面的切平面与法线
设曲面方程为 \(F\left( {x,y,z}\right) = 0\) ,其中 \(F\left( {x,y,z}\right)\) 具有连续的偏导数 \({F}_{x}^{\prime },{F}_{y}^{\prime },{F}_{z}^{\prime }\) ,且它们不同时为零. 则在曲面上点 \({M}_{0}\left( {{x}_{0},{y}_{0},{z}_{0}}\right)\) 处的切平面方程为\[{F}_{x}^{\prime }\left( {{x}_{0},{y}_{0},{z}_{0}}\right) \left( {x - {x}_{0}}\right) + {F}_{y}^{\prime }\left( {{x}_{0},{y}_{0},{z}_{0}}\right) \left( {y - {y}_{0}}\right) + {F}_{z}^{\prime }\left( {{x}_{0},{y}_{0},{z}_{0}}\right) \left( {z - {z}_{0}}\right) = 0\]法线方程为\[\frac{x - {x}_{0}}{{F}_{x}^{\prime }\left( {{x}_{0},{y}_{0},{z}_{0}}\right) } = \frac{y - {y}_{0}}{{F}_{y}^{\prime }\left( {{x}_{0},{y}_{0},{z}_{0}}\right) } = \frac{z - {z}_{0}}{{F}_{z}^{\prime }\left( {{x}_{0},{y}_{0},{z}_{0}}\right) }\]若曲面方程为 \(z = f\left( {x,y}\right)\) ,且 \(f\left( {x,y}\right)\) 具有连续的偏导数,则曲面上点 \({M}_{0}\left( {{x}_{0},{y}_{0},{z}_{0}}\right)\) 处的切平面方程为\[{f}_{x}^{\prime }\left( {{x}_{0},{y}_{0}}\right) \left( {x - {x}_{0}}\right) + {f}_{y}^{\prime }\left( {{x}_{0},{y}_{0}}\right) \left( {y - {y}_{0}}\right) - \left( {z - {z}_{0}}\right) = 0\]法线方程为\[\frac{x - {x}_{0}}{{f}_{x}^{\prime }\left( {{x}_{0},{y}_{0}}\right) } = \frac{y - {y}_{0}}{{f}_{y}^{\prime }\left( {{x}_{0},{y}_{0}}\right) } = \frac{z - {z}_{0}}{-1}\]
7. 方向导数与梯度
1. 方向导数
设函数 \(z = f\left( {x,y}\right)\) 在点 \(P\left( {x,y}\right)\) 的某个邻域内有定义,过点 \(P\) 引射线 \(l\) (如图 8-7-1 所示),在 \(l\) 上点 \(P\) 的邻近取一动点\[{P}^{\prime }\left( {x + {\Delta x},y + {\Delta y}}\right)\]
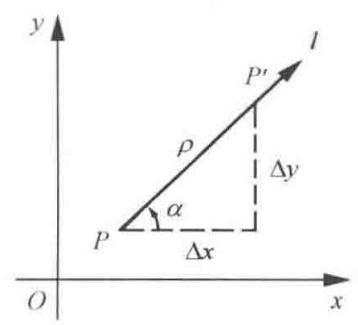
记 \(P\) 与 \({P}^{\prime }\) 的距离为\[\rho = \sqrt{{\left( \Delta x\right) }^{2} + {\left( \Delta y\right) }^{2}}\]当 \({P}^{\prime }\) 沿 \(l\) 趋于 \(P\) 时,如果极限\[\mathop{\lim }\limits_{{{P}^{\prime } \rightarrow P}}\frac{f\left( {P}^{\prime }\right) - f\left( P\right) }{\left| P{P}^{\prime }\right| } = \mathop{\lim }\limits_{{\rho \rightarrow 0}}\frac{f\left( {x + {\Delta x},y + {\Delta y}}\right) - f\left( {x,y}\right) }{\rho }\]存在,则称此极限值为函数 \(z = f\left( {x,y}\right)\) 在点 \(P\) 沿方向 \(l\) 的方向导数, 记为 \(\frac{\partial z}{\partial l}\)
当函数 \(z = f\left( {x,y}\right)\) 在点 \(P\left( {x,y}\right)\) 处可微,射线 \(l\) 的方向余弦为 \(\cos \alpha ,\cos \beta\) 时\[\frac{\partial z}{\partial l} = \frac{\partial z}{\partial x} \cdot \cos \alpha + \frac{\partial z}{\partial y} \cdot \cos \beta\]同样,三元函数 \(u = f\left( {x,y,z}\right)\) 在点 \(P\left( {x,y,z}\right)\) 处可微时,则沿方向余弦为 \(\cos \alpha ,\cos \beta ,\cos \gamma\) 的射线 \(l\) 的方向导数为\[\frac{\partial u}{\partial l} = \frac{\partial u}{\partial x} \cdot \cos \alpha + \frac{\partial u}{\partial y} \cdot \cos \beta + \frac{\partial u}{\partial z} \cdot \cos \gamma\]2. 梯度
设函数 \(z = f\left( {x,y}\right)\) 具有连续的一阶偏导数,则函数 \(z\) 在 \(P\left( {x,y}\right)\) 处的梯度是一个向量,记为 \(\operatorname{grad}z\) ,它在 \(x,y\) 坐标轴上的投影分别为在该点处的偏导数 \(\displaystyle\frac{\partial z}{\partial x}\) 与 \(\displaystyle\frac{\partial z}{\partial y}\) ,即\[\operatorname{grad}z = \frac{\partial z}{\partial x}\vu{i} + \frac{\partial z}{\partial y}\vu{j}\]函数 \(z = f\left( {x,y}\right)\) 在点 \(P\left( {x,y}\right)\) 处沿 \(l\) 方向上的方向导数 \(\displaystyle\frac{\partial z}{\partial l}\) ,等于函数在该点处的梯度 \(\operatorname{grad}z\) 在 \(l\) 方向上的投影,即\[\frac{\partial z}{\partial l} = \operatorname{grad}z \cdot {\va{l}}^{ \circ }\]其中, \({\va{l}}^{ \circ }\) 是射线 \(l\) 方向上的单位向量.
函数 \(z = f\left( {x,y}\right)\) 在点 \(P\) 处的梯度 \(\operatorname{grad}z\) 的模是函数 \(z\) 在该点处方向导数的最大值,它的方向与函数 \(z\) 在点 \(P\) 处取得最大方向导数的方向一致.
同样,三元函数 \(u = f\left( {x,y,z}\right)\) 具有连续的一阶偏导数时,函数 \(u\) 在点 \(P\left( {x,y,z}\right)\) 处的梯度为\[\operatorname{grad}u = \frac{\partial u}{\partial x}\vu{i} + \frac{\partial u}{\partial y}\vu{j} + \frac{\partial u}{\partial z}\vu{k}\]
8. 多元函数的极值及其求法
1. 极值
(1)极值的定义 设函数 \(z = f\left( {x,y}\right)\) 在点 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 的某个邻域内有定义,对于该邻域内异于 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 的点 \(P\left( {x,y}\right)\) ,如果都满足不等式 \(f\left( {x,y}\right) < f\left( {{x}_{0},{y}_{0}}\right)\) ,则称函数在点 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 处有极大值 \(f\left( {{x}_{0},{y}_{0}}\right)\) ; 如果都满足不等式 \(f\left( {x,y}\right) > f\left( {{x}_{0},{y}_{0}}\right)\) ,则称函数在点 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 处有极小值 \(f\left( {{x}_{0},{y}_{0}}\right)\) . 极大值、极小值统称为极值. 使函数取得极值的点称为极值点.
(2)极值存在的必要条件 若函数 \(z = f\left( {x,y}\right)\) 在点 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 处可微且取得极值,则必有 \({f}_{x}^{\prime }\left( {{x}_{0},{y}_{0}}\right) = 0,{f}_{y}^{\prime }\left( {{x}_{0},{y}_{0}}\right) = 0\)
(3)极值存在的充分条件 设函数 \(z = f\left( {x,y}\right)\) 在点 \({P}_{0}\left( {{x}_{0},{y}_{0}}\right)\) 的某邻域内具有二阶连续偏导数,且 \({f}_{x}^{\prime }\left( {{x}_{0},{y}_{0}}\right) = 0\) , \({f}_{y}^{\prime }\left( {{x}_{0},{y}_{0}}\right) = 0\) ,记 \(A = {f}_{xx}^{\prime \prime }\left( {{x}_{0},{y}_{0}}\right) ,B = {f}_{xy}^{\prime \prime }\left( {{x}_{0},{y}_{0}}\right) ,C = {f}_{yy}^{\prime \prime }\left( {{x}_{0},{y}_{0}}\right)\)
① 若 \({AC} -{B}^{2} > 0\) ,则 \(f\left( {{x}_{0},{y}_{0}}\right)\) 是极值,当 \(A < 0\) 时, \(f\left( {{x}_{0},{y}_{0}}\right)\) 是极大值,当 \(A > 0\) 时, \(f\left( {{x}_{0},{y}_{0}}\right)\) 是极小值.
② 若 \({AC} -{B}^{2} < 0\) ,则 \(f\left( {{x}_{0},{y}_{0}}\right)\) 不是极值.
③ 若 \({AC} -{B}^{2} = 0\) ,则 \(f\left( {{x}_{0},{y}_{0}}\right)\) 可能是极值,也可能不是极值.
2. 条件极值、拉格朗日乘数法
函数 \(u = f\left( {x,y}\right)\) 在附加条件 \(\varphi \left( {x,y}\right) = 0\) 下的极值称为条件极值.拉格朗日乘数法 求条件极值时, 可作函数\[F\left( {x,y,\lambda }\right) = f\left( {x,y}\right) + {\lambda \varphi }\left( {x,y}\right)\]其中, \(\lambda\) 是某一常数,则点(x, y)是极值点的必要条件为\[\left\{ \begin{array}{l} {F}_{x}^{\prime }\left( {x,y}\right) = {f}_{x}^{\prime }\left( {x,y}\right) + \lambda {\varphi }_{x}^{\prime }\left( {x,y}\right) = 0 \\ {F}_{y}^{\prime }\left( {x,y}\right) = {f}_{y}^{\prime }\left( {x,y}\right) + \lambda {\varphi }_{y}^{\prime }\left( {x,y}\right) = 0 \\ \varphi \left( {x,y}\right) = 0 \end{array}\right.\]从上述方程组中解出 \(x,y\) 及 \(\lambda\) 的值,则点(x, y)就可能是条件极值的极值点.
3. 函数的最大值和最小值
若二元函数 \(f\left( {x,y}\right)\) 在有界闭域 \(D\) 上连续,则 \(f\left( {x,y}\right)\) 在 \(D\) 上必定能取得最大值和最小值.
求函数最大值、最小值的一般方法是把函数 \(f\left( {x,y}\right)\) 在区域 \(D\) 内部的所有可能的极值点处的函数值连同边界上的函数值加以比较, 最大者为最大值, 最小者为最小值.
如果根据实际问题的性质已经知道函数的最大值 (最小值)一定在区域 \(D\) 内部取得,而函数在区域 \(D\) 内只有唯一驻点,则该驻点处的函数值就是函数 \(f\left( {x,y}\right)\) 在区域 \(D\) 上的最大值 (最小值).
9. 二元函数的泰勒公式
设函数 \(z = f\left( {x,y}\right)\) 在点 \(\left( {{x}_{0},{y}_{0}}\right)\) 的某一邻域内连续且有直到 \(\left( {n + 1}\right)\) 阶的连续偏导数,并设 \(\left( {x = {x}_{0} + h,y = {y}_{0} + k}\right)\) 为此邻域内任意一点,我们有二元函数的 \(n\) 阶泰勒公式\[f\left( {{x}_{0} + h,{y}_{0} + k}\right) = f\left( {{x}_{0},{y}_{0}}\right) + \left( {h\frac{\partial }{\partial x} + k\frac{\partial }{\partial y}}\right) f\left( {{x}_{0},{y}_{0}}\right)\]\[+ \frac{1}{2!}{\left( h\frac{\partial }{\partial x} + h\frac{\partial }{\partial y}\right) }^{2}f\left( {{x}_{0},{y}_{0}}\right) + \cdots + \frac{1}{n!}{\left( h\frac{\partial }{\partial x} + h\frac{\partial }{\partial y}\right) }^{n}f\left( {{x}_{0},{y}_{0}}\right) + {R}_{n}\qquad \text{①}\]其中\[{R}_{n} = \frac{1}{\left( {n + 1}\right) !}{\left( h\frac{\partial }{\partial x} + k\frac{\partial }{\partial y}\right) }^{n + 1}f\left( {{x}_{0} + {\theta h},y + {\theta k}}\right) ,\;0 < \theta < 1\]叫做拉格朗日形式的余项. 特别地,当 \(n = 0\) 时,公式①成为\[f\left( {{x}_{0} + h,{y}_{0} + k}\right) = f\left( {{x}_{0},{y}_{0}}\right) + h{f}_{x}^{\prime }\left( {{x}_{0} + {\theta h},{y}_{0} + {\theta k}}\right) + k{f}_{y}^{\prime }\left( {{x}_{0} + {\theta h},{y}_{0} + {\theta k}}\right)\]它叫做二元函数的拉格朗日中值定理.
又当 \(n = 1\) 时,公式①成为\[f\left( {{x}_{0} + h,{y}_{0} + k}\right) = f\left( {{x}_{0},{y}_{0}}\right) + h{f}_{x}^{\prime }\left( {{x}_{0},{y}_{0}}\right) + k{f}_{y}^{\prime }\left( {{x}_{0},{y}_{0}}\right) + \frac{1}{2!}\left\{ {{h}^{2}{f}_{xx}^{\prime \prime }\left( {{x}_{0} + {\theta h},{y}_{0} + {\theta k}}\right) }\right.\]\[\left. {+{2hk}{f}_{xy}^{\prime \prime }\left( {{x}_{0} + {\theta h},{y}_{0} + {\theta k}}\right) + {k}^{2}{f}_{yy}^{\prime \prime }\left( {{x}_{0} + {\theta h},{y}_{0} + {\theta k}}\right) }\right\} ,\;0 < \theta < 1\]



