1. 随机变量与分布函数
1. 随机变量
设 \(E\) 是一个随机试验,其样本空间为 \(\Omega = \{ \omega \}\) ,如果对于每一个样本点 \(\omega \in \Omega\) , 都有唯一的一个实数 \(X\left( \omega \right)\) 与之对应,则称 \(X\left( \omega \right)\) 为一维随机变量. 通常用 \(X,Y,Z,\cdots\) 表示随机变量
2. 分布函数
设 \(X\) 是一个随机变量, \(x\) 是任意实数,则函数 \(F\left( x\right) = P\{ X \leq x\}\) 称为 \(X\) 的分布函数
基本性质:
(1)单调性: \(F\left( x\right)\) 是一个单调不减的函数,即当 \({x}_{1} < {x}_{2}\) 时, \(F\left( {x}_{1}\right) \leq F\left( {x}_{2}\right)\)
(2)有界性: \(0 \leq F\left( x\right) \leq 1\) ,且\[F\left( {+\infty }\right) = \mathop{\lim }\limits_{{x \rightarrow + \infty }}F\left( x\right) = 1\]\[F\left( {-\infty }\right) = \mathop{\lim }\limits_{{x \rightarrow - \infty }}F\left( x\right) = 0\](3)连续性: \(F\left( {x + 0}\right) = F\left( x\right)\) ,即 \(F\left( x\right)\) 是右连续函数
3. 由分布函数求概率\[P\{ a < X \leq b\} = P\{ X \leq b\} - P\{ X \leq a\} = F\left( b\right) - F\left( a\right)\]
2. 离散型随机变量及其分布
1. 一维离散型随机变量
若随机变量 \(X\) 的全部可能取值是有限个或可列个,则称 \(X\) 为离散型随机变量
2. 分布律
离散型随机变量 \(X\) 所有可能取值为 \({x}_{k}\left( {k = 1,2,\cdots }\right)\) ,事件 \(\left\{ {X = {x}_{k}}\right\}\) 的概率为 \(P\left\{ {X = {x}_{k}}\right\} = {p}_{k}\) \(\left( {k = 1,2,\cdots }\right)\) ,则称 \(P\left\{ {X = {x}_{k}}\right\} = {p}_{k}\left( {k = 1,2,\cdots }\right)\) 为 \(X\) 的分布律或分布列. 分布律也可以写成表格形式:

离散型随机变量的分布律的性质:
(1)\(P\left\{ {X = {x}_{k}}\right\} = {p}_{k} \geq 0,k = 1,2,\cdots\)
(2)\(\mathop{\sum }\limits_{k}P\left\{ {X = {x}_{k}}\right\} = \mathop{\sum }\limits_{k}{p}_{k} = 1\)
3. 离散型随机变量 \(X\) 的分布律与分布函数以及事件概率的关系
(1)如果已知 \(X\) 的分布律为 \(P\left\{ {X = {x}_{k}}\right\} = {p}_{k}\left( {k = 1,2,\cdots }\right)\) ,则 \(X\) 的分布函数\[F\left( x\right) = P\{ X \leq x\} = \mathop{\sum }\limits_{{{x}_{k} \leq x}}{p}_{k}\]而事件 \(\{ a < X \leq b\}\) 的概率为\[P\{ a < X \leq b\} = \mathop{\sum }\limits_{{a < {x}_{k} \leq b}}{p}_{k}\](2)如果已知 \(X\) 的分布函数 \(F\left( x\right)\) ,则 \(X\) 的分布律为\[P\left\{ {X = {x}_{k}}\right\} = F\left( {x}_{k}\right) - F\left( {{x}_{k} - 0}\right) ,\;k = 1,2,\cdots\]4. 重要分布
(1)(0 - 1)分布: 其分布律为
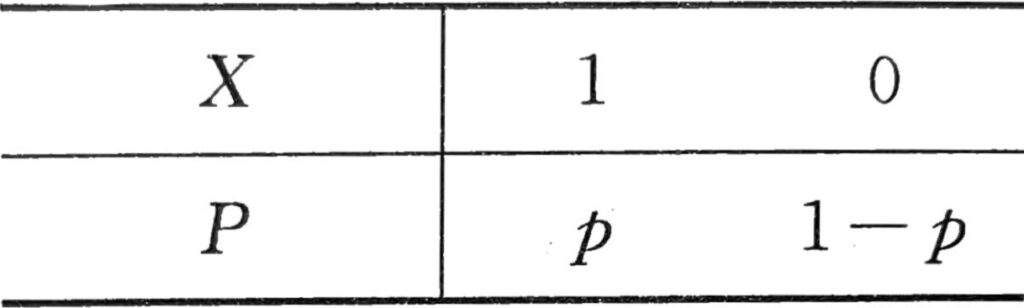
其中 \(p\) 为事件 \(A\) 出现的概率, \(0 < p < 1\)
(2)二项分布: 设在 \(n\) 重伯努利试验中事件 \(A\) 发生的次数为 \(X\) ,则\[P\{ X = k\} = {C}_{n}^{k}{p}^{k}{q}^{n - k},\;k = 0,1,2,\cdots \cdots ,n\]其中 \(p\) 为事件 \(A\) 在每次试验中出现的概率, \(q = 1 - p\) ,称随机变量 \(X\) 服从二项分布,记为\[X \sim B\left( {n,p}\right)\](3)泊松分布: 设随机变量 \(X\) 的分布律为:\[P\{ X = k\} = \frac{{\lambda }^{k}{\mathrm{e}}^{-\lambda }}{k!}\;\left( {k = 0,1,2,\cdots }\right)\]其中 \(\lambda > 0\) 是常数,则称 \(X\) 服从参数为 \(\lambda\) 的泊松分布,记为 \(X \sim \pi \left( \lambda \right)\) 或 \(P\left( \lambda \right)\)
泊松定理: 设随机变量 \({X}_{n} \sim B\left( {n,{p}_{n}}\right)\) ,若 \(\mathop{\lim }\limits_{{n \rightarrow \infty }}n{p}_{n} = \lambda > 0\) ,则有\[\mathop{\lim }\limits_{{n \rightarrow \infty }}{C}_{n}^{i}{p}_{n}^{i}{\left( 1 - {p}_{n}\right) }^{n - i} = \frac{{\lambda }^{i}}{i!}{\mathrm{e}}^{-\lambda }\;\left( {i = 1,2,\cdots }\right)\]由泊松定理, 二项分布可以用泊松分布作为近似
(4)超几何分布: 设随机变量 \(X\) 的分布列是\[P\{ X = i\} = \frac{{C}_{M}^{i}{C}_{N - M}^{n - i}}{{C}_{N}^{n}},\;\left( {i = 0,1,2,\cdots ,l;l = \min \{ n,M\} }\right)\]其中 \(M\text{ 、 }N\text{ 、 }n\) 都是自然数,且 \(n < N,M < N\) ,则称 \(X\) 服从参数为 \(N\text{ 、 }M\text{ 、 }n\) 的超几何分布,记作 \(X \sim\) \(H\left( {N,M,n}\right)\)
(5)几何分布: 设随机变量 \(X\) 的分布列为\[P\{ X = i\} = {\left( 1 - p\right) }^{i - 1}p,\;i = 1,2,3,\cdots \]其中 \(0 < p < 1\) ,则称 \(X\) 服从参数为 \(p\) 的几何分布,记为 \(X \sim G\left( p\right)\)
3. 连续型随机变量及其分布
1. 连续型随机变量的概率密度
如果对于随机变量 \(X\) 的分布函数 \(F\left( x\right)\) ,存在非负可积函数 \(f\left( x\right)\) ,使得对任意实数 \(x\) ,有 \(\displaystyle F\left( x\right) = {\int }_{-\infty }^{x}f\left( t\right) \mathrm{d}t\) 成立,则称 \(X\) 为连续型随机变量,函数 \(f\left( x\right)\) 称为 \(X\) 的概率密度 (或分布密度)
2. 连续型随机变量的概率密度函数 \(f\left( x\right)\) 的性质
(1)\(f\left( x\right) \geq 0\)
(2)\(\displaystyle {\int }_{-\infty }^{+\infty }f\left( x\right) \mathrm{d}x = 1\)
3. 连续型随机变量的概率密度与分布函数以及事件概率的关系
(1)若 \(X\) 的概率密度为 \(f\left( x\right)\) ,则 \(X\) 的分布函数为 \(\displaystyle F\left( x\right) = {\int }_{-\infty }^{x}f\left( t\right) \mathrm{d}t\) ,当 \(f\left( x\right)\) 为分段函数时其分布函数 \(F\left( x\right)\) 要做分段讨论
(2)若 \(f\left( x\right)\) 在点 \(x\) 处连续,则有 \({F}^{\prime }\left( x\right) = f\left( x\right)\)
(3) \(P\{ a < X \leq b\} = P\{ a < X < b\} = P\{ a \leq X < b\} = P\{ a \leq X \leq b\}\)\(\displaystyle = F\left( b\right) - F\left( a\right) = {\int }_{a}^{b}f\left( x\right) \mathrm{d}x\)
(4)\(P\{ X = a\} = 0\left( {-\infty < a < + \infty }\right)\)
4. 重要分布
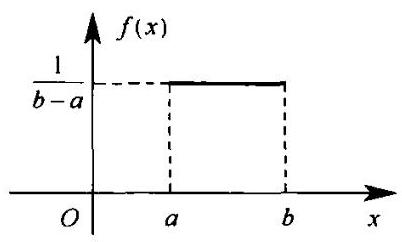
(1)均匀分布: 若连续型随机变量 \(X\) 的概率密度函数为\[f\left( x\right) = \left\{ {\begin{matrix} \frac{1}{b - a}, & a \leq x \leq b \\ 0, & \text{ 其他 } \end{matrix}\;}\right. \;\text{ (如图 2-3-1) }\]则称 \(X\) 服从 \(\left\lbrack {a,b}\right\rbrack\) 上的均匀分布
(2)指数分布: 若连续型随机变量 \(X\) 的概率密度函数为\[f\left( x\right) = \left\{ \begin{array}{ll} \lambda {\mathrm{e}}^{-{\lambda x}}, & x > 0 \\ 0, & \text{ 其他 } \end{array}\right. \;\text{ (如图 2-3-2) }\]
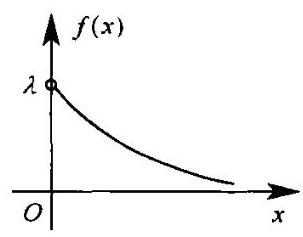
其中 \(\lambda > 0\) ,则称 \(X\) 服从参数为 \(\lambda\) 的指数分布
(3)正态分布: 若连续型随机变量 \(X\) 的概率密度函数为\[f\left( x\right) = \frac{1}{\sqrt{2\pi }\sigma }{\mathrm{e}}^{-\frac{{\left( x - \mu \right) }^{2}}{2{\sigma }^{2}}}\;\left( {-\infty < x < + \infty }\right) \;\text{ (如图 }2-3-3\text{ ) }\]
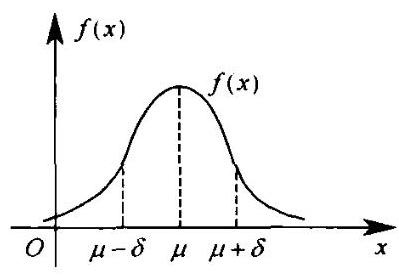
其中 \(\mu\) 与 \(\sigma > 0\) 都是常数,则称 \(X\) 服从参数为 \(\mu\) 和 \(\sigma\) 的正态分布. 简记为 \(X \sim N\left( {\mu ,{\sigma }^{2}}\right)\)
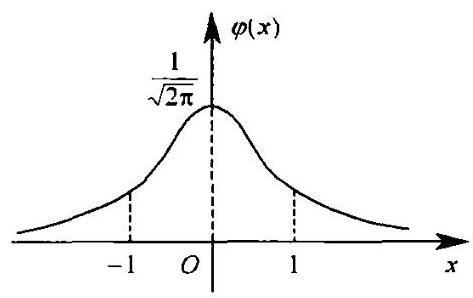
(4)标准正态分布: 当 \(\mu = 0,\sigma = 1\) 时称 \(X\) 服从标准正态分布,简记为 \(X \sim N\left( {0,1}\right)\) ,其概率密度函数和分布函数分别用 \(\varphi \left( x\right) ,\Phi \left( x\right)\) 表示,即有\[\varphi \left( x\right) = \frac{1}{\sqrt{2\pi }}{\mathrm{e}}^{-\frac{{x}^{2}}{2}}\;\left( {\text{ 如图 }2-3-4}\right)\]\[\Phi \left( x\right) = \frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^{x}{\mathrm{e}}^{-\frac{{t}^{2}}{2}}\mathrm{d}t\]性质 1 \({\Phi }\left( {-x}\right) = 1 - \Phi \left( x\right)\)
性质 2 当 \(X \sim N\left( {\mu ,{\sigma }^{2}}\right)\) 时, \(\displaystyle U = \frac{X - \mu }{\sigma } \sim N\left( {0,1}\right)\) . 即 \(\displaystyle F\left( x\right) = \Phi \left( \frac{x - \mu }{\sigma }\right)\)
4. 随机变量函数的分布
1. 离散型随机变量函数的分布
设随机变量 \(X\) 的分布律为 \(P\left\{ {X = {x}_{k}}\right\} = {p}_{k},k = 1,2,3\cdots\) ,则当 \(Y = g\left( X\right)\) 的所有取值为 \({y}_{j}\) \(\left( {j = 1,2,\cdots }\right)\) 时,随机变量 \(Y\) 有分布律\[P\left\{ {Y = {y}_{j}}\right\} = \mathop{\sum }\limits_{{g\left( {x}_{k}\right) = {y}_{j}}}P\left\{ {X = {x}_{k}}\right\}\]2. 连续型随机变量函数的分布
方法一: 设随机变量 \(X\) 的概率密度函数为 \({f}_{X}\left( x\right) \left( {-\infty < x < + \infty }\right)\) ,那么 \(Y = g\left( X\right)\) 的分布函数为\[{F}_{Y}\left( y\right) = P\{ Y \leq y\} = P\{ g\left( X\right) \leq y\} = {\int }_{g\left( x\right) \leq y}{f}_{X}\left( x\right) \mathrm{d}x\]其概率密度为 \({f}_{Y}\left( y\right) = {F}_{Y}^{\prime }\left( y\right)\)
方法二: 设随机变量 \(X\) 具有概率密度函数 \({f}_{X}\left( x\right) \left( {-\infty < x < + \infty }\right) ,g\left( x\right)\) 为 \(\left( {-\infty , + \infty }\right)\) 内的严格单调的可导函数,则随机变量 \(Y = g\left( X\right)\) 的概率密度为\[{f}_{Y}\left( y\right) = \left\{ \begin{array}{ll} {f}_{X}\left\lbrack {h\left( y\right) }\right\rbrack \left| {{h}^{\prime }\left( y\right) }\right| , & \alpha < y < \beta \\ 0, & \text{ 其他 } \end{array}\right.\]其中 \(h\left( y\right)\) 是 \(g\left( x\right)\) 的反函数, \(\alpha = \min \{ g\left( {-\infty }\right) ,g\left( {+\infty }\right) \} ,\beta = \max \{ g\left( {-\infty }\right) ,g\left( {+\infty }\right) \}\)



