1. 总体
是指研究对象的某个性能指标的全体,通常用一随机变量 \(X\) 代表总体
2. 个体 是指每一个研究对象
3. 样本 从总体中取 \(n\) 个个体,称作来自总体的容量为 \(n\) 的样本
简单随机样本 是指 \(n\) 个相互独立,而且与总体 \(X\) 同分布的随机变量 \({X}_{1},{X}_{2},\cdots ,{X}_{n}\) ,简称随机样本,也常以随机向量 \(\left( {{X}_{1},{X}_{2},\cdots ,{X}_{n}}\right)\) 表示. 它们的一组观察值 \({x}_{1},{x}_{2},\cdots ,{x}_{n}\) 称为样本值
4. 统计量 称不含未知参数的样本函数 \(g\left( {{X}_{1},{X}_{2},\cdots ,{X}_{n}}\right)\) 为统计量
常见统计量
\(\displaystyle \bar{X} = \frac{1}{n}\mathop{\sum }\limits_{{i = 1}}^{n}{X}_{i}\) 为样本均值
\(\displaystyle {S}^{2} = \frac{1}{n - 1}\mathop{\sum }\limits_{{i = 1}}^{n}{\left( {X}_{i} - \bar{X}\right) }^{2}\) 为样本方差
\(\displaystyle S = \sqrt{{S}^{2}}\) 称为样本标准差
\(\displaystyle {A}_{k} = \frac{1}{n}\mathop{\sum }\limits_{{i = 1}}^{n}{X}_{i}^{k}\) 为 \(k\) 阶样本原点矩
\(\displaystyle {B}_{k} = \frac{1}{n}\mathop{\sum }\limits_{{i = 1}}^{n}{\left( {X}_{i} - \bar{X}\right) }^{k}\) 为 \(k\) 阶样本中心矩
其中 \(\displaystyle {B}_{2} = {S}_{n}^{2} = \frac{1}{n}\mathop{\sum }\limits_{{i = 1}}^{n}{\left( {X}_{i} - \bar{X}\right) }^{2} = \frac{n - 1}{n}{S}^{2}\)
5. 经验分布函数
从总体 \(X\) 中抽取一个容量为 \(n\) 的样本,将其观察值 \(\left( {{x}_{1},{x}_{2},\cdots ,{x}_{n}}\right)\) 按大小顺序,重新排列如下\[{x}_{1}^{ * } \leq {x}_{2}^{ * } \leq \cdots \leq {x}_{n}^{ * }\]对于任意的实数 \(x\) ,定义函数\[{F}_{n}\left( x\right) = \left\{ \begin{array}{ll} 0, & x < {x}_{1}^{ * } \\ \frac{k}{n}, & {x}_{k}^{ * } \leq x < {x}_{k + 1}^{ * },\;k = 1,2,\cdots ,n - 1 \\ 1, & {x}_{n}^{ * } \leq x \end{array}\right.\]称 \({F}_{n}\left( x\right)\) 为总体 \(X\) 由 \({x}_{1},{x}_{2},\cdots ,{x}_{n}\) 所决定的样本分布函数或经验分布函数
格列汶科定理 当 \(n \rightarrow \infty\) 时, \({F}_{n}\left( x\right)\) 依概率 1 关于 \(x\) 均匀地收敛于 \(F\left( x\right)\) . 即说明: 当 \(n\) 很大时,样本分布函数 \({F}_{n}\left( x\right)\) 近似于总体分布函数 \(F\left( x\right)\)
6. \({\chi }^{2}\) 分布
(1)定义: 设随机变量 \({X}_{1},\cdots ,{X}_{n}\) 相互独立同分布 \(N\left( {0,1}\right)\) ,若有 \({\chi }^{2} = \mathop{\sum }\limits_{{i = 1}}^{n}{X}_{i}^{2}\) ,则随机变量 \({\chi }^{2}\)的分布称为 \(n\) 个自由度的 \({\chi }^{2}\) 分布. 即 \({\chi }^{2} \sim {\chi }^{2}\left( n\right)\) . 其概率密度函数为\[\varphi \left( x\right) = \left\{ \begin{array}{ll} \frac{1}{{2}^{\frac{n}{2}}\Gamma \left( \frac{n}{2}\right) }{x}^{\frac{n}{2} - 1}{\mathrm{e}}^{-\frac{x}{2}}, & x > 0 \\ 0, & x \leq 0 \end{array}\right.\]用图形表示其密度函数为图 6-1
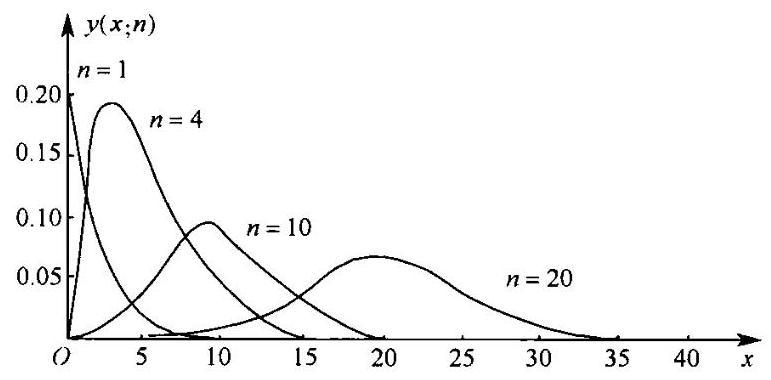
(2)性质:
① \(E\left( {{\chi }^{2}\left( n\right) }\right) = n,D\left( {{\chi }^{2}\left( n\right) }\right) = {2n}\)
② 设 \(X \sim {\chi }^{2}\left( m\right) ,Y \sim {\chi }^{2}\left( n\right)\) ,且 \(X\) 与 \(Y\) 相互独立. 则\[X + Y \sim {\chi }^{2}\left( {m + n}\right)\](3)上 \(\alpha\) 分位点:对于给定的正数 \(\alpha \left( {0 < \alpha < 1}\right)\) ,称满足条件\[P\left\{ {{\chi }^{2} > {\chi }_{\alpha }^{2}\left( n\right) }\right\} = \alpha\]的点 \({\chi }_{\alpha }^{2}\left( n\right)\) 为 \({\chi }^{2}\) 分布的上 \(\alpha\) 分位点
7. \(t\) 分布
(1)定义: 设随机变量 \(X\) 与 \(Y\) 相互独立. \(X \sim N\left( {0,1}\right) ,Y \sim {\chi }^{2}\left( n\right)\) ,若 \(\displaystyle T = \frac{X}{\sqrt{\frac{Y}{n}}}\) ,则随机变量 \(T\) 的分布称为 \(n\) 个自由度的 \(t\) 分布,即 \(T \sim t\left( n\right)\) ,其概率密度函数为\[\varphi \left( x\right) = \frac{\Gamma \left( \frac{n + 1}{2}\right) }{\sqrt{n\pi }\Gamma \left( \frac{n}{2}\right) }{\left( 1 + \frac{{x}^{2}}{n}\right) }^{-\frac{n + 1}{2}}\;\left( {-\infty < x < + \infty }\right)\]用图形表示其概率密度为图 6-2
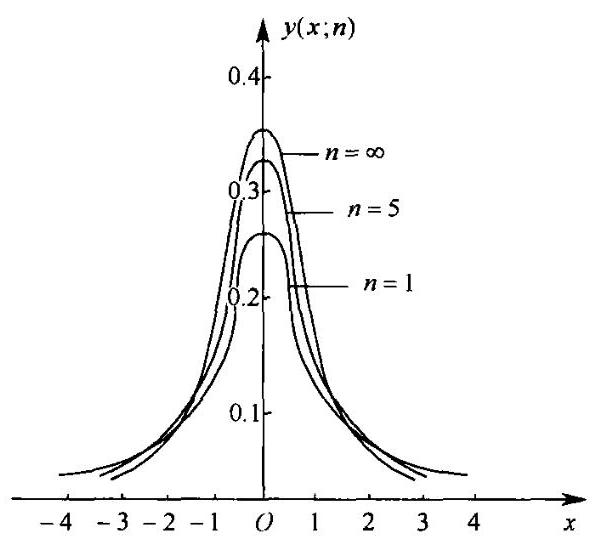
(2)性质:
①\(\displaystyle E\left( {t\left( n\right) }\right) = 0,D\left( {t\left( n\right) }\right) = \frac{n}{n - 2}\;\left( {n > 2}\right)\)
②\(\displaystyle \mathop{\lim }\limits_{{n \rightarrow \infty }}\varphi \left( x\right) = \frac{1}{\sqrt{2\pi }}{\mathrm{e}}^{-\frac{{x}^{2}}{2}}\) ,故 \(n\) 足够大时, \(t\) 分布近似于 \(N\left( {0,1}\right)\)
③若 \(T \sim t\left( n\right)\) ,则 \({T}^{2} \sim F\left( {1,n}\right)\)
(3)上 \(\alpha\) 分位点: \(t\left( n\right)\) 分布的上 \(\alpha\) 分位点 \({t}_{\alpha }\left( n\right)\) 是指满足\[P\left\{ {T > {t}_{\alpha }\left( n\right) }\right\} = \alpha \;\left( {0 < \alpha < 1}\right) \;\text{ 的点 }{t}_{\alpha }\left( n\right)\]其中 \({t}_{1 - \alpha }\left( n\right) = - {t}_{\alpha }\left( n\right)\)
8. \(F\) 分布
(1)定义: 设随机变量 \(X\) 与 \(Y\) 相互独立,且分别服从 \(\displaystyle {\chi }^{2}\left( m\right)\) 和 \(\displaystyle {\chi }^{2}\left( n\right)\) 分布,若 \(\displaystyle F = \frac{\frac{X}{m}}{\frac{Y}{n}}\) ,则 \(F\) 服从自由度为 \(m,n\) 的 \(F\) 分布. 即 \(F \sim F\left( {m,n}\right)\) ,其概率密度函数为\[\large \varphi \left( x\right) = \left\{ \begin{array}{ll} \frac{\Gamma \left( \frac{m + n}{2}\right) }{\Gamma \left( \frac{m}{2}\right) \Gamma \left( \frac{n}{2}\right) }{m}^{\frac{m}{2}}{n}^{\frac{n}{2}}\frac{{x}^{\frac{m}{2} - 1}}{{\left( mx + n\right) }^{\frac{m + n}{2}}}, & x > 0 \\ 0, & x \leq 0 \end{array}\right.\]用图形表示其概率密度函数为图 6-3
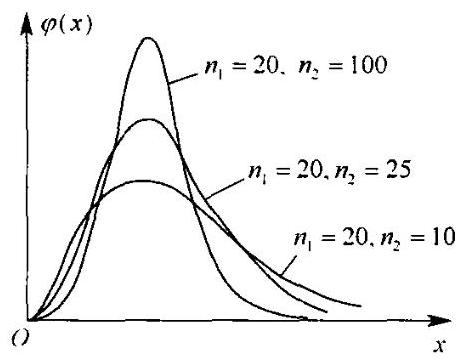
(2)性质:
①若 \(X \sim F\left( {m,n}\right)\) ,则\[E\left( X\right) = \frac{n}{n - 2}\;\left( {n > 2}\right)\]\[D\left( X\right) = \frac{{n}^{2}\left( {{2m} + {2n} - 4}\right) }{m{\left( n - 2\right) }^{2}\left( {n - 4}\right) }\;\left( {n > 4}\right)\]②若 \(X \sim F\left( {m,n}\right)\) ,则 \(\displaystyle \frac{1}{X} \sim F\left( {n,m}\right)\)
(3)上 \(\alpha\) 分位点:满足 \(P\left\{ {F > {F}_{\alpha }\left( {m,n}\right) }\right\} = \alpha \;\left( {0 < \alpha < 1}\right)\) 的点 \({F}_{\alpha }\left( {m,n}\right)\) 称为上 \(\alpha\) 分位点,且 \(\displaystyle {F}_{1 - \alpha }\left( {m,n}\right) = \frac{1}{{F}_{\alpha }\left( {n,m}\right) }\)
9. 正态总体的常用结论
(1)若总体 \(X\) 服从正态分布 \(N\left( {\mu ,{\sigma }^{2}}\right) ,{X}_{1},\cdots ,{X}_{n}\) 是其样本, \(\bar{X}\) 和 \({S}^{2}\) 分别为样本均值和方差, 则
①\(\displaystyle \bar{X} \sim N\left( {\mu ,\frac{{\sigma }^{2}}{n}}\right)\) 或 \(\displaystyle \frac{\bar{X} - \mu }{\sigma }\sqrt{n} \sim N\left( {0,1}\right)\)
②\(\displaystyle \frac{\left( {n - 1}\right) {S}^{2}}{{\sigma }^{2}} \sim {\chi }^{2}\left( {n - 1}\right)\)
③\(\displaystyle \frac{\bar{X} - \mu }{S}\sqrt{n} \sim t\left( {n - 1}\right)\)
④\(\bar{X}\) 与 \({S}^{2}\) 相互独立
(2)若 \({X}_{1},{X}_{2},\cdots ,{X}_{n}\) 和 \({Y}_{1},{Y}_{2},\cdots ,{Y}_{m}\) 分别表示取自两个正态总体 \(N\left( {{\mu }_{1},{\sigma }_{1}^{2}}\right)\) 和 \(N\left( {{\mu }_{2},{\sigma }_{2}^{2}}\right)\) 的简单随机样本, \(\bar{X},\bar{Y}\) 和 \({S}_{1}^{2},{S}_{2}^{2}\) 分别表示其样本均值和方差,则有
①\(\displaystyle \frac{\frac{{S}_{1}^{2}}{{\sigma }_{1}^{2}}}{\frac{{S}_{2}^{2}}{{\sigma }_{2}^{2}}} \sim F\left( {n - 1,m - 1}\right)\)
②\(\displaystyle \sqrt{\frac{{mn}\left( {n + m - 2}\right) }{n + m}}\frac{\left( {\bar{X} - \bar{Y}}\right) - \left( {{\mu }_{1} - {\mu }_{2}}\right) }{\sqrt{\left( {n - 1}\right) {S}_{1}^{2} + \left( {m - 1}\right) {S}_{2}^{2}}} \sim t\left( {n + m - 2}\right)\) . (当 \({\sigma }_{1}^{2} = {\sigma }_{2}^{2}\) 时)



