1. 二维随机变量及其分布
1. 二维随机变量
设 \(E\) 是随机试验,样本空间 \(\Omega = \{ \omega \}\) ,由 \(X = X\left( \omega \right) ,Y = Y\left( \omega \right)\) 构成的向量 (X, Y)称为二维随机变量
2. 联合分布函数
设(X, Y)是二维随机变量, \(x,y\) 是两个任意实数,则称定义在平面上的二元函数 \(P\{ X \leq x,Y \leq y\}\) 为(X, Y)的分布函数,或称为 \(X\) 和 \(Y\) 的联合分布函数,记作 \(F\left( {x,y}\right)\) ,即\[F\left( {x,y}\right) = P\{ X \leq x,Y \leq y\}\]\(F\left( {x,y}\right)\) 的性质:
(1)\(0 \leq F\left( {x,y}\right) \leq 1\) ,且 \(F\left( {-\infty ,y}\right) = F\left( {x, - \infty }\right) = F\left( {-\infty , - \infty }\right) = 0,F\left( {+\infty , + \infty }\right) = 1\)
(2)\(F\left( {x,y}\right)\) 是变量 \(x\) 或 \(y\) 的单调不减函数
(3)\(F\left( {x,y}\right) = F\left( {x + 0,y}\right) ,F\left( {x,y}\right) = F\left( {x,y + 0}\right) ,F\left( {x,y}\right)\) 关于 \(x\) 或 \(y\) 都是右连续的
(4)对任意 \(\left( {{x}_{1},{y}_{1}}\right) ,\left( {{x}_{2},{y}_{2}}\right)\) : 当 \({x}_{1} < {x}_{2},{y}_{1} < {y}_{2}\) 时有
\(P\left\{ {{x}_{1} < X \leq {x}_{2},{y}_{1} < Y \leq {y}_{2}}\right\} = F\left( {{x}_{2},{y}_{2}}\right) - F\left( {{x}_{1},{y}_{2}}\right) - F\left( {{x}_{2},{y}_{1}}\right) + F\left( {{x}_{1},{y}_{1}}\right)\)
3. 二维离散型随机变量
若(X, Y)所有可能取值为 \(\left( {{x}_{i},{y}_{j}}\right) ,i,j = 1,2,\cdots\) ,则 \(P\left\{ {X = {x}_{i},Y}\right.\) \(\left. { = {y}_{j}}\right\} = {p}_{ij}\) 称为联合分布律,联合分布律可列表如下:
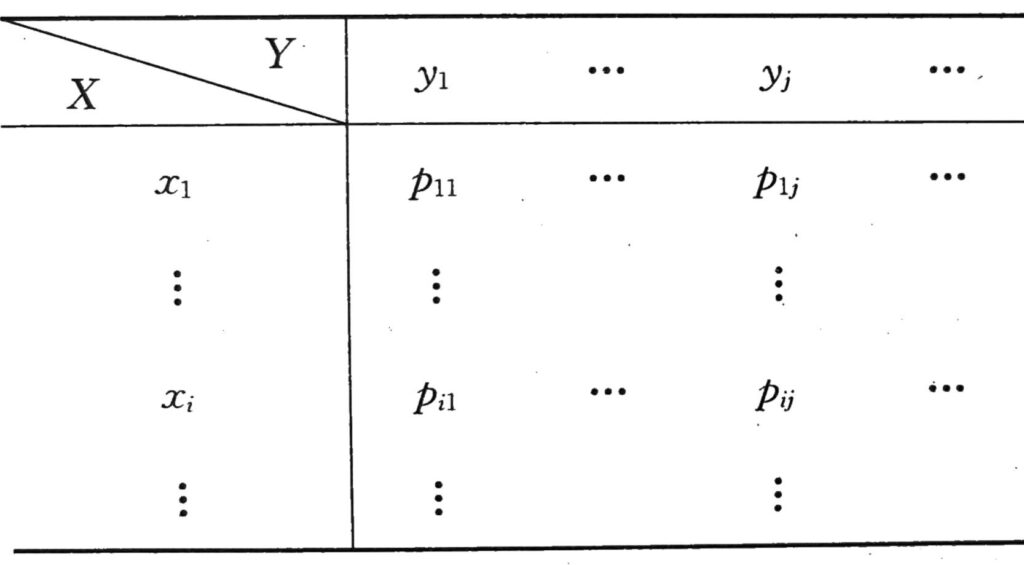
联合分布律的性质: \(\displaystyle {p}_{ij} \geq 0,\mathop{\sum }\limits_{{i = 1}}^{\infty }\mathop{\sum }\limits_{{j = 1}}^{\infty }{p}_{ij} = 1\)
4. 二维连续型随机变量
若分布函数 \(\displaystyle F\left( {x,y}\right) = {\int }_{-\infty }^{x}{\int }_{-\infty }^{y}f\left( {u,v}\right) \mathrm{d}u\mathrm{\;d}v\) ,则称(X, Y)是连续型随机变量. \(f\left( {x,y}\right)\) 称为(X, Y)的联合概率密度
联合概率密度的性质:
(1)\(\displaystyle f\left( {x,y}\right) \geq 0;\;{\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }f\left( {x,y}\right) \mathrm{d}x\mathrm{d}y = 1\)
(2)若 \(f\left( {x,y}\right)\) 在点(x, y)处连续,则 \(\displaystyle \frac{{\partial }^{2}F\left( {x,y}\right) }{\partial x\partial y} = f\left( {x,y}\right)\)
(3) 设 \(G\) 是 \({xOy}\) 平面上一个区域,则 \(\displaystyle P\{ \left( {X,Y}\right) \in G\} = {\iint }_{G}f\left( {x,y}\right) \mathrm{d}x\mathrm{d}y\)
2. 边缘分布
1. 边缘分布函数
设二维随机变量(X, Y)的分布函数为 \(F\left( {x,y}\right)\) ,分别称函数
\({F}_{X}\left( x\right) = \mathop{\lim }\limits_{{y \rightarrow + \infty }}F\left( {x,y}\right) = F\left( {x, + \infty }\right) \;\) 和 \(\;{F}_{Y}\left( y\right) = \mathop{\lim }\limits_{{x \rightarrow + \infty }}F\left( {x,y}\right) = F\left( {+\infty ,y}\right)\)
为(X, Y)关于 \(X\) 和 \(Y\) 的边缘分布函数
2. 边缘分布律
设二维离散型随机变量(X, Y)的联合分布律为 \(P\left\{ {X = {x}_{i},Y = {y}_{j}}\right\} = {p}_{ij}\) ,则分别称\[{p}_{i \cdot} = \mathop{\sum }\limits_{{j = 1}}^{\infty }{p}_{ij} = P\left\{ {X = {x}_{i}}\right\} \;\left( {i = 1,2,3,\cdots }\right)\]和\[p_{\cdot j} = \mathop{\sum }\limits_{{i = 1}}^{\infty }{p}_{ij} = P\left\{ {Y = {y}_{j}}\right\} \;\left( {j = 1,2,3,\cdots \cdots }\right)\]为(X, Y)关于 \(X\) 和 \(Y\) 的边缘分布律
3. 边缘概率密度
设二维连续型随机变量(X, Y)的概率密度为 \(f\left( {x,y}\right)\) ,则 \({f}_{X}\left( x\right) =\) \({\int }_{-\infty }^{+\infty }f\left( {x,y}\right) \mathrm{d}y\) 和 \({f}_{Y}\left( y\right) = {\int }_{-\infty }^{+\infty }f\left( {x,y}\right) \mathrm{d}x\) 分别称为(X, Y)关于 \(X\) 和 \(Y\) 的边缘概率密度
4. 常用的二维分布
(1)二维均匀分布: 如果二维随机变量(X, Y)有概率密度\[f\left( {x,y}\right) = \left\{ \begin{array}{ll} \frac{1}{A}, & \left( {x,y}\right) \in G \\ 0, & \text{ 其他. } \end{array}\right.\]其中 \(G\) 为平面有界区域, \(A\) 为其面积,则称(X, Y)在 \(G\) 上服从二维均匀分布
(2)二维正态分布: 如果二维随机变量(X, Y)的概率密度为\[\small f\left( {x,y}\right) = \frac{1}{{2\pi }{\sigma }_{1}{\sigma }_{2}\sqrt{1 - {\rho }^{2}}}\exp \left\{ {-\frac{1}{2\left( {1 - {\rho }^{2}}\right) }\left\lbrack {\frac{{\left( x - {\mu }_{1}\right) }^{2}}{{\sigma }_{1}^{2}} - {2\rho }\frac{\left( {x - {\mu }_{1}}\right) \left( {y - {\mu }_{2}}\right) }{{\sigma }_{1}{\sigma }_{2}} + \frac{{\left( y - {\mu }_{2}\right) }^{2}}{{\sigma }_{2}^{2}}}\right\rbrack }\right\}\]其中 \({\mu }_{1},{\mu }_{2},{\sigma }_{1},{\sigma }_{2},\rho\) 均为常数,且 \({\sigma }_{1} > 0,{\sigma }_{2} > 0, - 1 < \rho < 1\) ,则称(X, Y)服从参数为 \({\mu }_{1},{\mu }_{2},{\sigma }_{1},{\sigma }_{2}\) , \(\rho\) 的二维正态分布,记作\[\left( {X,Y}\right) \sim N\left( {{\mu }_{1},{\sigma }_{1}^{2};{\mu }_{2},{\sigma }_{2}^{2};\rho }\right)\]特别, 当 \({\mu }_{1} = {\mu }_{2} = 0,{\sigma }_{1} = {\sigma }_{2} = 1\) 时,则称(X, Y)服从标准正态分布
性质: \(\left( {X,Y}\right) \sim N\left( {{\mu }_{1},{\sigma }_{1}^{2};{\mu }_{2},{\sigma }_{2}^{2};\rho }\right) \Rightarrow X \sim N\left( {{\mu }_{1},{\sigma }_{1}^{2}}\right) ,Y \sim N\left( {{\mu }_{2},{\sigma }_{2}^{2}}\right)\) . 逆命题不成立
3. 条件分布
1. 条件分布律
设(X, Y)是二维离散型随机变量,若 \(p_{\cdot j} > 0\) ,则称\[{p}_{X \mid Y}\left( {i \mid j}\right) = P\left\{ {X = {x}_{i} \mid Y = {y}_{j}}\right\} = \frac{{p}_{ij}}{p_{\cdot j}}\;\left( {i = 1,2,\cdots }\right)\]为在 \(\left\{ {Y = {y}_{j}}\right\}\) 条件下随机变量 \(X\) 的条件分布律
若 \({p}_{i\cdot}> 0\) ,则称\[{p}_{Y \mid X}\left( {j \mid i}\right) = P\left\{ {Y = {y}_{j} \mid X = {x}_{i}}\right\} = \frac{{p}_{ij}}{{p}_{i\cdot}}\;\left( {j = 1,2,\cdots }\right)\]为在 \(\left\{ {X = {x}_{i}}\right\}\) 条件下随机变量 \(Y\) 的条件分布律
2. 条件概率密度
设(X, Y)是二维连续型随机变量,若 \({f}_{Y}\left( y\right) > 0\) ,则称\[{f}_{X \mid Y}\left( {x \mid y}\right) = \frac{f\left( {x,y}\right) }{{f}_{Y}\left( y\right) }\;\left( {-\infty < x < + \infty }\right)\]为在 \(\{ Y = y\}\) 条件下 \(X\) 的条件概率密度
若 \({f}_{X}\left( x\right) > 0\) ,则称\[{f}_{Y \mid X}\left( {y \mid x}\right) = \frac{f\left( {x,y}\right) }{{f}_{X}\left( x\right) }\;\left( {-\infty < y < + \infty }\right)\]为在 \(\{ X = x\}\) 条件下 \(Y\) 的条件概率密度
4. 随机变量的独立性
1. 随机变量的独立性
若二维随机变量(X, Y)对任意实数均有
\(P\{ X \leq x,Y \leq y\} = P\{ X \leq x\} P\{ Y \leq y\} ,\;\) 即 \(F\left( {x,y}\right) = {F}_{X}\left( x\right) \cdot {F}_{Y}\left( y\right)\)
则 \(X\) 与 \(Y\) 相互独立
2. 离散型随机变量相互独立的充要条件\[{p}_{ij} = {p}_{i\cdot} p_{\cdot j},\;i,j = 1,2,\cdots\]3. 连续型随机变量相互独立的充要条件\[f\left( {x,y}\right) = {f}_{X}\left( x\right) \cdot {f}_{Y}\left( y\right) ,\;x,y\text{ 任意实数 }\]
5. 多维随机变量函数的分布
1. 二维随机变量函数的分布
(1)已知离散型随机变量(X, Y)的分布律 \(P\left\{ {X = {x}_{i},Y = {y}_{j}}\right\} = {p}_{ij}\) ,则 \(Z = g\left( {X,Y}\right)\) 的分布为\[P\left\{ {Z = {z}_{k}}\right\} = P\left\{ {g\left( {X,Y}\right) = {z}_{k}}\right\} = \mathop{\sum }\limits_{{g\left( {{x}_{i},{y}_{j}}\right) = {z}_{k}}}{p}_{ij}\](2)设连续型随机变量(X, Y)的概率密度为 \(f\left( {x,y}\right)\) ,则 \(Z = g\left( {X,Y}\right)\) 的分布函数为\[{F}_{Z}\left( z\right) = P\{ Z \leq z\} = {\iint }_{g\left( {x,y}\right) \leq z}f\left( {x,y}\right) \mathrm{d}x\mathrm{d}y\]概率密度 \({f}_{Z}\left( z\right) = {F}_{Z}^{\prime }\left( z\right)\)
特殊类型:
①\(Z = X + Y\) 密度函数为\[{f}_{Z}\left( z\right) = {\int }_{-\infty }^{+\infty }f\left( {x,z - x}\right) \mathrm{d}x = {\int }_{-\infty }^{+\infty }f\left( {z - y,y}\right) \mathrm{d}y\]特别, 当 \(X\) 与 \(Y\) 相互独立时\[{f}_{Z}\left( z\right) = {f}_{X} * {f}_{Y} = {\int }_{-\infty }^{+\infty }{f}_{X}\left( x\right) {f}_{Y}\left( {z - x}\right) \mathrm{d}x = {\int }_{-\infty }^{+\infty }{f}_{X}\left( {z - y}\right) {f}_{Y}\left( y\right) \mathrm{d}y\]②设 \(X \sim N\left( {{\mu }_{1},{\sigma }_{1}^{2}}\right) ,Y \sim N\left( {{\mu }_{2},{\sigma }_{2}^{2}}\right)\) ,且 \(X,Y\) 相互独立,则\[{aX} + {bY} \sim N\left( {a{\mu }_{1} + b{\mu }_{2},{a}^{2}{\sigma }_{1}^{2} + {b}^{2}{\sigma }_{2}^{2}}\right)\]③设 \(X,Y\) 相互独立,分布函数分别为 \({F}_{X}\left( x\right)\) 和 \({F}_{Y}\left( y\right) ,M = \max \left( {X,Y}\right) ,N = \min \left( {X,Y}\right)\) ,则\[{F}_{M}\left( z\right) = {F}_{X}\left( z\right) {F}_{Y}\left( z\right)\]\[{F}_{N}\left( z\right) = 1 - \left\lbrack {1 - {F}_{X}\left( z\right) }\right\rbrack \left\lbrack {1 - {F}_{Y}\left( z\right) }\right\rbrack\]④\(Z = \frac{X}{Y}\) 的密度函数为\[{f}_{Z}\left( z\right) = {\int }_{-\infty }^{+\infty }\left| y\right| f\left( {{yz},y}\right) \mathrm{d}y\]当 \(X,Y\) 相互独立时,\[{f}_{Z}\left( z\right) = {\int }_{-\infty }^{+\infty }\left| y\right| {f}_{X}\left( {yz}\right) {f}_{Y}\left( y\right) \mathrm{d}y\]⑤\(Z = \frac{Y}{X}\) 的密度函数为\[{f}_{Z}\left( z\right) = {\int }_{-\infty }^{+\infty }\left| x\right| f\left( {x,{xz}}\right) \mathrm{d}x\]当 \(X,Y\) 相互独立时,\[{f}_{Z}\left( z\right) = {\int }_{-\infty }^{+\infty }\left| x\right| {f}_{X}\left( x\right) {f}_{Y}\left( {xz}\right) \mathrm{d}x\]⑥\(Z = {XY}\) 的密度函数为\[{f}_{Z}\left( z\right) = {\int }_{-\infty }^{+\infty }\frac{1}{\left| x\right| }f\left( {x,\frac{z}{x}}\right) \mathrm{d}x\]当 \(X,Y\) 相互独立时,\[{f}_{Z}\left( z\right) = {\int }_{-\infty }^{+\infty }\frac{1}{\left| x\right| }{f}_{X}\left( x\right) {f}_{Y}\left( \frac{z}{x}\right) \mathrm{d}x\]2. 多维随机变量函数的分布
对于相互独立的多维随机变量所构成的简单函数, 可利用二维随机变量的结果加以推广. 常用结论及公式如下:
(1)设 \({X}_{1},{X}_{2},\cdots ,{X}_{n}\) 相互独立,且 \({X}_{i} \sim N\left( {{\mu }_{i},{\sigma }_{i}^{2}}\right) ,{k}_{i}\) 为任意常数, \(\left( {i = 1,2,\cdots ,n}\right)\) ,则\[Z = \mathop{\sum }\limits_{{i = 1}}^{n}{k}_{i}{X}_{i} \sim N\left( {\mathop{\sum }\limits_{{i = 1}}^{n}{k}_{i}{\mu }_{i},\mathop{\sum }\limits_{{i = 1}}^{n}{k}_{i}^{2}{\sigma }_{i}^{2}}\right)\](2)设 \({X}_{1},{X}_{2},\cdots ,{X}_{n}\) 相互独立,且 \({X}_{i}\) 的分布函数为 \({F}_{{X}_{i}}\left( {x}_{i}\right) \left( {i = 1,2,\cdots ,n}\right)\) ,则 \(Z =\) \(\max \left\{ {{X}_{1},{X}_{2},\cdots ,{X}_{n}}\right\}\) 的分布函数为\[{F}_{\max }\left( z\right) = {F}_{{X}_{1}}\left( z\right) {F}_{{X}_{2}}\left( z\right) \cdots {F}_{{X}_{n}}\left( z\right)\]\(Z = \min \left\{ {{X}_{1},{X}_{2},\cdots ,{X}_{n}}\right\}\) 的分布函数为\[{F}_{\min }\left( z\right) = 1 - \left\lbrack {1 - {F}_{{X}_{1}}\left( z\right) }\right\rbrack \left\lbrack {1 - {F}_{{X}_{2}}\left( z\right) }\right\rbrack \cdots \left\lbrack {1 - {F}_{{X}_{n}}\left( z\right) }\right\rbrack\]



