1. 二重积分
1. 二重积分的概念
函数 \(f\left( {x,y}\right)\) 在二维有界闭区域 \(D\) 上的二重积分系指下述和式的极限:\[{\iint }_{D}f\left( {x,y}\right) \mathrm{d}x\mathrm{\;d}y = \mathop{\lim }\limits_{{\lambda \rightarrow 0}}\mathop{\sum }\limits_{{i = 1}}^{n}f\left( {{\xi }_{i},{\eta }_{i}}\right) \Delta {\sigma }_{i}\]其中 \(\Delta {\sigma }_{i}\) 是分割区域 \(D\) 为 \(n\) 个子区域 \({\sigma }_{1},{\sigma }_{2},\cdots ,{\sigma }_{n}\) 时子区域 \({\sigma }_{i}\) 的面积,而 \(\left( {{\xi }_{i},{\eta }_{i}}\right) \in {\sigma }_{i},\lambda\) 为各子区域 \({\sigma }_{i}\left( {i = 1,2,\cdots ,n}\right)\) 直径之最大者.
若 \(f\left( {x,y}\right)\) 在 \(D\) 上连续,则上述二重积分存在.
2. 二重积分的性质
性质 1 \(\displaystyle{\iint }_{D}{kf}\left( {x,y}\right) \mathrm{d}\sigma = k{\iint }_{D}f\left( {x,y}\right) \mathrm{d}\sigma\) ,其中 \(k\) 为常数
性质 2 \(\displaystyle{\iint }_{D}\left\lbrack {{f}_{1}\left( {x,y}\right) \pm {f}_{2}\left( {x,y}\right) }\right\rbrack \mathrm{d}\sigma = {\iint }_{D}{f}_{1}\left( {x,y}\right) \mathrm{d}\sigma \pm {\iint }_{D}{f}_{2}\left( {x,y}\right) \mathrm{d}\sigma\)
性质 3 若有界闭区域 \(D\) 能分为两个闭区域 \({D}_{1}\) 与 \({D}_{2}\) ,则\[{\iint }_{D}f\left( {x,y}\right) \mathrm{d}\sigma = {\iint }_{{D}_{1}}f\left( {x,y}\right) \mathrm{d}\sigma + {\iint }_{{D}_{2}}f\left( {x,y}\right) \mathrm{d}\sigma\]即二重积分对于积分区域具有可加性.
性质 4 (二重积分的保号性) 若在区域 \(D\) 上, \(f\left( {x,y}\right) \leq \varphi \left( {x,y}\right)\) ,则\[{\iint }_{D}f\left( {x,y}\right) \mathrm{d}\sigma \leq {\iint }_{D}\varphi \left( {x,y}\right) \mathrm{d}\sigma\]性质 5 (二重积分的估值定理) 设在有界闭区域 \(D\) 上 \(f\left( {x,y}\right)\) 的最大值和最小值分别为 \(M\) 和 \(m\) ,则\[{m\sigma } \leq {\iint }_{D}f\left( {x,y}\right) \mathrm{d}\sigma \leq {M\sigma }\]其中 \(\sigma\) 是区域 \(D\) 的面积.
性质 6 (二重积分的中值定理) 设函数 \(f\left( {x,y}\right)\) 在有界闭区域 \(D\) 上连续,则在 \(D\) 上至少存在一点 \(\left( {\xi ,\eta }\right)\) ,使得\[{\iint }_{D}f\left( {x,y}\right) \mathrm{d}\sigma = f\left( {\xi ,\eta }\right) \sigma\]其中, \(\sigma\) 表示区域 \(D\) 的面积.
3. 二重积分计算法
(1)在直角坐标系中的计算法 在直角坐标系中,二重积分的面积元素 \(\mathrm{d}\sigma\) 可写成 \(\mathrm{d}x\mathrm{\;d}y\) ,于是\[{\iint }_{D}f\left( {x,y}\right) \mathrm{d}\sigma = {\iint }_{D}f\left( {x,y}\right) \mathrm{d}x\mathrm{\;d}y\]如果积分区域 \(D\) 是由两条直线 \(x = a,x = b\) 与两条曲线 \(y = {\varphi }_{1}\left( x\right) ,y = {\varphi }_{2}\left( x\right)\) 所围成(如图 9-1-1 所示).
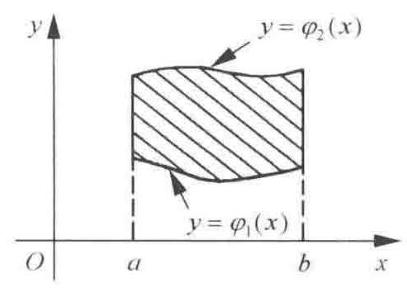
即 \(D : \left\{ \begin{array}{l} a \leq x \leq b \\ {\varphi }_{1}\left( x\right) \leq y \leq {\varphi }_{2}\left( x\right) \end{array}\right.\)
则 \(\displaystyle{\iint }_{D}f\left( {x,y}\right) \mathrm{d}x\mathrm{\;d}y = {\int }_{a}^{b}\mathrm{\;d}x{\int }_{{\varphi }_{1}\left( x\right) }^{{\varphi }_{2}\left( x\right) }f\left( {x,y}\right) \mathrm{d}y\)
如果积分区域 \(D\) 是由两条直线 \(y = c,y = d\) 与两条曲线 \(x =\) \({\psi }_{1}\left( y\right) ,x = {\psi }_{2}\left( y\right)\) 所围成(如图 9-1-2 所示)
即 \(D : \left\{ \begin{array}{l} c \leq y \leq d \\ {\psi }_{1}\left( y\right) \leq x \leq {\psi }_{2}\left( y\right) \end{array}\right.\)
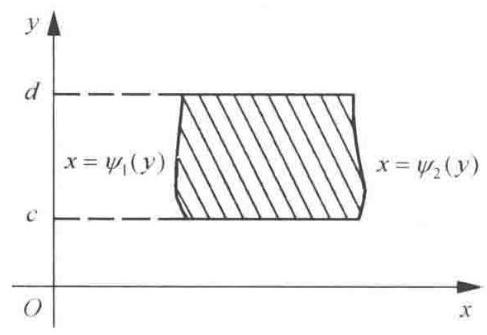
则 \(\displaystyle{\iint }_{D}f\left( {x,y}\right) \mathrm{d}x\mathrm{\;d}y = {\int }_{c}^{d}\mathrm{\;d}y{\int }_{{\psi }_{1}\left( y\right) }^{{\psi }_{2}\left( y\right) }f\left( {x,y}\right) \mathrm{d}x\)
(2)在极坐标系中的计算法 在极坐标系中 \(\left\{ \begin{array}{l} x = r\cos \theta \\ y = r\sin \theta \end{array}\right.\) ,面积元素 \(\mathrm{d}\sigma = r\mathrm{d}r\mathrm{d}\theta\)
如果极点 \(O\) 不在区域 \(D\) 上,而区域 \(D\) 是由两条射线 \(\theta = \alpha ,\theta = \beta\) 与两条曲线 \(r = {r}_{1}\left( \theta \right) ,r = {r}_{2}\left( \theta \right)\) 所围成 (如 \(9-1-3\) 所示)
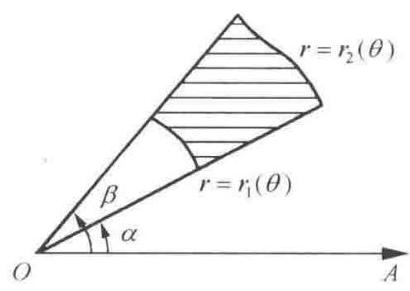
即 \(D : \left\{ \begin{array}{l} \alpha \leq \theta \leq \beta \\ {r}_{1}\left( \theta \right) \leq r \leq {r}_{2}\left( \theta \right) \end{array}\right.\)
则 \(\displaystyle{\iint }_{D}f\left( {x,y}\right) \mathrm{d}\sigma = {\int }_{\alpha }^{\beta }\mathrm{d}\theta {\int }_{{r}_{1}\left( \theta \right) }^{{r}_{2}\left( \theta \right) }f\left( {r\cos \theta ,r\sin \theta }\right) r\mathrm{\;d}r\)
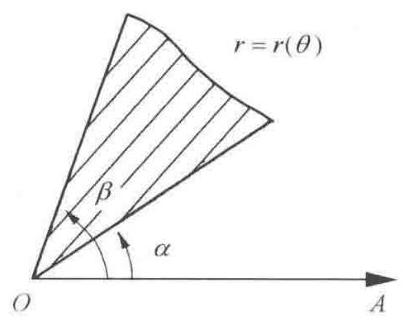
如果区域 \(D\) 是曲边扇形 (如图 9-1-4 所示),即 \(D : \left\{ \begin{array}{l} \alpha \leq \theta \leq \beta \\ 0 \leq r \leq r\left( \theta \right) \end{array}\right.\)
则 \(\displaystyle{\iint }_{D}f\left( {x,y}\right) \mathrm{d}\sigma = {\int }_{\alpha }^{\beta }\mathrm{d}\theta {\int }_{0}^{r\left( \theta \right) }f\left( {r\cos \theta ,r\sin \theta }\right) r\mathrm{\;d}r\)
如果区域 \(D\) 由闭曲线 \(r = r\left( \theta \right)\) 所围成,且极点 \(O\) 在区域 \(D\) 内 (如图 9-1-5 所示),
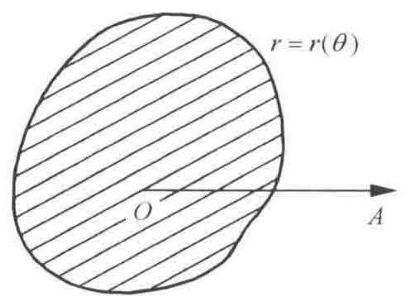
则 \(\displaystyle{\iint }_{D}f\left( {x,y}\right) \mathrm{d}\sigma = {\int }_{0}^{2\pi }\mathrm{d}\theta {\int }_{0}^{r\left( \theta \right) }f\left( {r\cos \theta ,r\sin \theta }\right) r\mathrm{d}r\)
2. 三重积分
1. 三重积分的概念
函数 \(f\left( {x,y,z}\right)\) 在三维有界闭区域 \(\Omega\) 上的三重积分系指下述和式的极限:\[{\iiint }_{\Omega }f\left( {x,y,z}\right) \mathrm{d}x\mathrm{\;d}y\mathrm{\;d}z = \mathop{\lim }\limits_{{\lambda \rightarrow 0}}\mathop{\sum }\limits_{{i = 1}}^{n}f\left( {{\xi }_{i},{\eta }_{i},{\zeta }_{i}}\right) \Delta {V}_{i}\]其中 \(\Delta {V}_{i}\) 是分割区域 \(\Omega\) 为 \(n\) 个子区域 \({V}_{1},{V}_{2},\cdots ,{V}_{n}\) 时子区域 \({V}_{i}\) 的体积,而 \(\left( {{\xi }_{i},{\eta }_{i},{\zeta }_{i}}\right) \in {V}_{i},\lambda\) 为各子区域 \({V}_{i}\left( {i = 1,2,\cdots ,n}\right)\) 直径之最大者.
若 \(f\left( {x,y,z}\right)\) 在 \(\Omega\) 上连续,则上述三重积分存在.
2. 三重积分的计算法
(1)在直角坐标系中的计算法 在直角坐标系中,三重积分的体积元素 \(\mathrm{d}V\) 为 \(\mathrm{d}x\mathrm{\;d}y\mathrm{\;d}z\) . 设空间有界闭区域 \(\Omega\) 在 \({xOy}\) 平面上的投影为 \({D}_{xy}\) ,且平行于 \(z\) 轴的直线与 \(\Omega\) 的边界曲面 \(S\) 的交点不多于两个. 此时如果 \(\Omega\) 可表示为:\[\Omega : \left\{ \begin{array}{l} a \leq x \leq b \\ {y}_{1}\left( x\right) \leq y \leq {y}_{2}\left( x\right) \\ {z}_{1}\left( {x,y}\right) \leq z \leq {z}_{2}\left( {x,y}\right) \end{array}\right.\]则\[{\iiint }_{\Omega }f\left( {x,y,z}\right) \mathrm{d}V = {\iiint }_{\Omega }f\left( {x,y,z}\right) \mathrm{d}x\mathrm{\;d}y\mathrm{\;d}z\]\[= {\iint }_{{D}_{xy}}\mathrm{\;d}x\mathrm{\;d}y{\int }_{{z}_{1}\left( {x,y}\right) }^{{z}_{2}\left( {x,y}\right) }f\left( {x,y,z}\right) \mathrm{d}z = {\int }_{a}^{b}\mathrm{\;d}x{\int }_{{y}_{1}\left( x\right) }^{{y}_{2}\left( x\right) }\mathrm{d}y{\int }_{{z}_{1}\left( {x,y}\right) }^{{z}_{2}\left( {x,y}\right) }f\left( {x,y,z}\right) \mathrm{d}z\]
(2)在柱面坐标系下的计算法 直角坐标与柱面坐标的关系是 \(\left\{ \begin{array}{l} x = r\cos \theta \\ y = r\sin \theta \\ z = z \end{array}\right.\)
在柱面坐标系中三重积分的体积元素 \(\mathrm{d}V\) 为 \(r\mathrm{d}r\mathrm{d}\theta \mathrm{d}z\) ,因此\[{\iiint }_{\Omega }f\left( {x,y,z}\right) \mathrm{d}V = {\iiint }_{\Omega }f\left( {r\cos \theta ,r\sin \theta ,z}\right) r\mathrm{d}r\mathrm{d}\theta \mathrm{d}z\]将右端化为累次积分, 即可求得其结果.
(3)在球面坐标系下的计算法 直角坐标与球面坐标的关系是 \(\left\{ \begin{array}{l} x = r\sin \varphi \cos \theta \\ y = r\sin \varphi \sin \theta \\ z = r\cos \varphi \end{array}\right.\)
在球面坐标系中三重积分的体积元素 \(\mathrm{d}V\) 为 \({r}^{2}\sin \varphi \mathrm{d}r\mathrm{d}\theta \mathrm{d}\varphi\) ,因此\[{\iiint }_{\Omega }f\left( {x,y,z}\right) \mathrm{d}V = {\iiint }_{\Omega }f\left( {r\sin \varphi \cos \theta ,r\sin \varphi \sin \theta ,r\cos \varphi }\right) {r}^{2}\sin \varphi \mathrm{d}r\mathrm{d}\varphi \mathrm{d}\theta\]将右端化为累次积分即可求得其结果.
3. 重积分的应用
1. 计算面积
(1)平面闭域面积为 \(\displaystyle A = {\iint }_{D}\mathrm{d}x\mathrm{d}y\)
(2)设曲面 \(\sum\) 的方程为 \(z = f\left( {x,y}\right) ,\sum\) 在 \({xOy}\) 平面上投影区域为 \(D,f\left( {x,y}\right)\) 在 \(D\) 上存在连续偏导数,则曲面 \(\sum\) 的面积为\[A = {\iint }_{D}\sqrt{1 + {\left( \frac{\partial z}{\partial x}\right) }^{2} + {\left( \frac{\partial z}{\partial y}\right) }^{2}}\mathrm{\;d}x\mathrm{d}y\]
2. 计算体积
(1)曲顶柱体的体积 设柱体上顶是连续的曲面 \(z = f\left( {x,y}\right) \left( {\left( {x,y}\right) \in D,f\left( {x,y}\right) \geq 0}\right)\) ,下底是平面 \(z = 0\) ,侧面为以区域 \(D\) 的边界曲线为准线而母线平行于 \(z\) 轴的柱面,则此柱体的体积为\[V = {\iint }_{D}f\left( {x,y}\right) \mathrm{d}x\mathrm{d}y\](2)已知边界曲面的空间区域 \(\Omega\) 的体积 \(\displaystyle V = {\iiint }_{\Omega }\mathrm{d}x\mathrm{d}y\mathrm{d}z\)
3. 静力矩和重心
(1)占有平面区域 \(D\) 且质量密度为 \(\displaystyle\mu \left( {x,y}\right)\) 的平面薄片质量 \(\displaystyle M = {\iint }_{D}\mu \left( {x,y}\right) {d\sigma }\) ,它对 \(x\) 轴、 \(y\) 轴的静力矩为\[{M}_{x} = {\iint }_{D}{y\mu }\left( {x,y}\right) \mathrm{d}\sigma ,\;{M}_{y} = {\iint }_{D}{x\mu }\left( {x,y}\right) \mathrm{d}\sigma\]\(D\) 的重心坐标为 \(\displaystyle\bar{x} = \frac{{M}_{y}}{M},\;\bar{y} = \frac{{M}_{x}}{M}\)
(2)占有空间区域 \(\Omega\) 且质量密度为 \(\mu \left( {x,y,z}\right)\) 的空间物体的重心坐标为:\[\left\{ \begin{array}{l} \bar{x} = \frac{1}{M}{\iiint }_{\Omega }{x\mu }\left( {x,y,z}\right) \mathrm{d}x\mathrm{d}y\mathrm{d}z \\ \bar{y} = \frac{1}{M}{\iiint }_{\Omega }{y\mu }\left( {x,y,z}\right) \mathrm{d}x\mathrm{d}y\mathrm{d}z \\ \bar{z} = \frac{1}{M}{\iiint }_{\Omega }{z\mu }\left( {x,y,z}\right) \mathrm{d}x\mathrm{d}y\mathrm{d}z \end{array}\right.\]其中 \(M\) 为 \(\Omega\) 的质量 \(\displaystyle M = {\iiint }_{\Omega }\mu \left( {x,y,z}\right) \mathrm{d}x\mathrm{d}y\mathrm{d}z\)



