1. 矩阵的运算
1. 矩阵的概念
由 \(m \times n\) 个数 \({a}_{ij}\left( {i = 1,2,\cdots ,m;j = 1,2,\cdots ,n}\right)\) 按一定次序排成的 \(m\) 行 \(n\) 列的矩形数表\[\left\lbrack \begin{matrix} {a}_{11} & {a}_{12} & \cdots & {a}_{1n} \\ {a}_{21} & {a}_{22} & \cdots & {a}_{2n} \\ \cdots & \cdots & \cdots & \cdots \\ {a}_{m1} & {a}_{m2} & \cdots & {a}_{mn} \end{matrix}\right\rbrack\]称为 \(m \times n\) 矩阵 ( \(m\) 行 \(n\) 列矩阵). \({a}_{ij}\) 叫做矩阵的元素,矩阵可简记为\[\boldsymbol{A} = {\left( {a}_{ij}\right) }_{m \times n}\text{ 或 }\boldsymbol{A} = \left( {a}_{ij}\right) \]当 \(m = n\) 时,即矩阵的行数与列数相同时,称 \(\boldsymbol{A}\) 为 \(n\) 阶方阵
当 \(m = 1\) 时,矩阵只有一行,称为行矩阵,记为\[\boldsymbol{A} = \left( {{a}_{11},{a}_{12},\cdots ,{a}_{1n}}\right)\]这样的行矩阵也称为 \(n\) 维行向量
当 \(n = 1\) 时,矩阵只有一列,称为列矩阵,记为\[\boldsymbol{A} = \left\lbrack \begin{matrix} {a}_{11} \\ {a}_{12} \\ \cdots \\ {a}_{m1} \end{matrix}\right\rbrack\]这样的列矩阵也称为 \(m\) 维列向量
矩阵 \(\boldsymbol{A}\) 中各元素变号得到的矩阵叫做 \(\boldsymbol{A}\) 的负矩阵,记作 \(- \boldsymbol{A}\) ,即\[- \boldsymbol{A} = {\left( -{a}_{ij}\right) }_{m \times n}\]如果矩阵 \(\boldsymbol{A}\) 的所有元素都是 0,即\[\boldsymbol{A} = \left\lbrack \begin{matrix} 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & 0 \end{matrix}\right\rbrack\]则 \(\boldsymbol{A}\) 称为零矩阵,记为0
2. 矩阵的运算
(1)矩阵的相等 设\[\boldsymbol{A} = {\left( {a}_{ij}\right) }_{m \times n},\;\boldsymbol{B} = {\left( {b}_{ij}\right) }_{m \times n}\]如果 \({a}_{ij} = {b}_{ij}\left( {i = 1,2,\cdots ,m;j = 1,2,\cdots ,n}\right)\) ,则称矩阵 \(\boldsymbol{A}\) 与 \(\boldsymbol{B}\) 相等,记作 \(\boldsymbol{A} = \boldsymbol{B}\)
(2)矩阵的加、减法 设\[\boldsymbol{A} = {\left( {a}_{ij}\right) }_{m \times n},\;\boldsymbol{B} = {\left( {b}_{ij}\right) }_{m \times n},\;\boldsymbol{C} = {\left( {c}_{ij}\right) }_{m \times n}\]其中 \({c}_{ij} = {a}_{ij} \pm {b}_{ij}\left( {i = 1,2,\cdots ,m;j = 1,2,\cdots ,n}\right)\)
则称 \(\boldsymbol{C}\) 为矩阵 \(\boldsymbol{A}\) 与 \(\boldsymbol{B}\) 的和 (或差),记为 \(\boldsymbol{C} = \boldsymbol{A} \pm \boldsymbol{B}\)
(3) 数与矩阵的乘法 设 \(k\) 为一个常数,\[\boldsymbol{A} = {\left( {a}_{ij}\right) }_{m \times n},\;\boldsymbol{C} = {\left( {c}_{ij}\right) }_{m \times n}\]其中 \({c}_{ij} = k{a}_{ij}\left( {i = 1,2,\cdots ,m;j = 1,2,\cdots ,n}\right)\)
则称矩阵 \(\boldsymbol{C}\) 为数 \(k\) 与矩阵 \(\boldsymbol{A}\) 的数量乘积,简称数乘,记为 \(k\boldsymbol{A}\)
(4)矩阵的乘法 设 \(\boldsymbol{A} = {\left( {a}_{ij}\right) }_{m \times s},\boldsymbol{B} = {\left( {b}_{ij}\right) }_{s \times n},\boldsymbol{C} = {\left( {c}_{ij}\right) }_{m \times n}\) ,其中\[{c}_{ij} = \mathop{\sum }\limits_{{l = 1}}^{s}{a}_{il}{b}_{lj}\;\left( {i = 1,2,\cdots ,m;j = 1,2,\cdots ,n}\right)\]则称矩阵 \(\boldsymbol{C}\) 为矩阵 \(\boldsymbol{A}\) 与 \(\boldsymbol{B}\) 的乘积,记为 \(\boldsymbol{{AB}}\) ,即 \(\boldsymbol{C} = \boldsymbol{{AB}}\)
(5)方阵的幂运算 对 \(n\) 阶方阵 \(\boldsymbol{A}\) ,定义\[{\boldsymbol{A}}^{k} = \underset{k\text{个}}{\underbrace{\boldsymbol{A} \cdot \boldsymbol{A} \cdot \cdots \cdot \boldsymbol{A}}}\text{ ,称为 }\boldsymbol{A}\text{ 的 }k\text{ 次幂.} \](6) 矩阵的转置 把矩阵 \(\boldsymbol{A} = {\left( {a}_{ij}\right) }_{m \times n}\) 的行列互换而得到的矩阵 \({\left( {a}_{ji}\right) }_{n \times m}\) 称为 \(\boldsymbol{A}\) 的转置矩阵, 记为 \({\boldsymbol{A}}^{T}\) (或 \({\boldsymbol{A}}^{\prime }\) )
(7)方阵的行列式 方阵 \(\boldsymbol{A}\) 的元素按原来的位置构成的行列式,称为方阵 \(\boldsymbol{A}\) 的行列式,记为 \(\left| \boldsymbol{A}\right|\)
若 \(\left| \boldsymbol{A}\right| = 0\) ,称 \(\boldsymbol{A}\) 为奇异矩阵,否则称为非奇异矩阵
3. 矩阵的运算公式
关于矩阵的加法运算公式
(1)\(\boldsymbol{A} + \boldsymbol{B} = \boldsymbol{B} + \boldsymbol{A}\)
(2)\(\left( {\boldsymbol{A} + \boldsymbol{B}}\right) + \boldsymbol{C} = \boldsymbol{A} + \left( {\boldsymbol{B} + \boldsymbol{C}}\right)\)
(3)\(\boldsymbol{A} + \left( {-\boldsymbol{A}}\right) = \boldsymbol{0}\)
(4)\(\left( {\boldsymbol{A} - \boldsymbol{B}}\right) = \boldsymbol{A} + \left( {-\boldsymbol{B}}\right)\)
关于数乘运算的公式
(1)\(\left( {kl}\right) \boldsymbol{A} = k\left( {l\boldsymbol{A}}\right)\)
(2)\(\left( {k + l}\right) \boldsymbol{A} = k\boldsymbol{A} + l\boldsymbol{A}\)
(3)\(k\left( {\boldsymbol{A} + \boldsymbol{B}}\right) = k\boldsymbol{A} + k\boldsymbol{B}\)
关于矩阵的乘法运算的公式
(1)\(\left( \boldsymbol{{AB}}\right) \boldsymbol{C} = \boldsymbol{A}\left( \boldsymbol{{BC}}\right)\)
(2)\(k\left( \boldsymbol{{AB}}\right) = \left( {k\boldsymbol{A}}\right) \boldsymbol{B} = \boldsymbol{A}\left( {k\boldsymbol{B}}\right)\)
(3)\(\boldsymbol{A}\left( {\boldsymbol{B} + \boldsymbol{C}}\right) = \boldsymbol{{AB}} + \boldsymbol{{AC}};\left( {\boldsymbol{B} + \boldsymbol{C}}\right) \boldsymbol{A} = \boldsymbol{{BA}} + \boldsymbol{{CA}}\)
(4)\(\boldsymbol{{EA}} = \boldsymbol{{AE}} = \boldsymbol{A}\)
(5)\(\left( {\lambda \boldsymbol{E}}\right) \boldsymbol{A} = \lambda \boldsymbol{A} = \boldsymbol{A}\left( {\lambda \boldsymbol{E}}\right)\)
(6)\({\boldsymbol{A}}^{k}{\boldsymbol{A}}^{l} = {\boldsymbol{A}}^{k + l}\)
(7)\({\left( {\boldsymbol{A}}^{k}\right) }^{l} = {\boldsymbol{A}}^{kl}\)
(8)矩阵的乘法一般不满足交换律,即 \(\boldsymbol{{AB}}\) 有意义,但 \(\boldsymbol{{BA}}\) 不一定有意义;即使 \(\boldsymbol{{AB}}\) 和 \(\boldsymbol{{BA}}\) 都有意义, 两者也不一定相等
(9)两个非零矩阵相乘,可能是零矩阵,从而不能从 \(\boldsymbol{{AB}} = \boldsymbol{0}\) 必然推出 \(\boldsymbol{A} = \boldsymbol{0}\) 或 \(\boldsymbol{B} = \boldsymbol{0}\)
(10)矩阵的乘法一般不满足消去律,即不能从 \(\boldsymbol{{AC}} = \boldsymbol{{BC}}\) 必然推出 \(\boldsymbol{A} = \boldsymbol{B}\)
关于矩阵的转置运算的公式
(1)\({\left( {\boldsymbol{A}}^{T}\right) }^{T} = \boldsymbol{A}\)
(2)\({\left( \boldsymbol{A} + \boldsymbol{B}\right) }^{T} = {\boldsymbol{A}}^{T} + {\boldsymbol{B}}^{T}\)
(3)\({\left( k\boldsymbol{A}\right) }^{T} = k{\boldsymbol{A}}^{T}\)
(4)\({\left( \boldsymbol{{AB}}\right) }^{T} = {\boldsymbol{B}}^{T}{\boldsymbol{A}}^{T}\)
关于方阵的行列式的公式
若 \(\boldsymbol{A}\text{ 、 }\boldsymbol{B}\) 是 \(n\) 阶方阵,
(1)\(\left| {\boldsymbol{A}}^{T}\right| = \left| \boldsymbol{A}\right|\)
(2)\(\left| {\lambda \boldsymbol{A}}\right| = {\lambda }^{n}\left| \boldsymbol{A}\right|\)
(3)\(\left| \boldsymbol{{AB}}\right| = \left| \boldsymbol{A}\right| \left| \boldsymbol{B}\right|\)
(4)\(\left| \boldsymbol{{AB}}\right| = \left| \boldsymbol{{BA}}\right|\)
4. 几类特殊矩阵
(1)单位矩阵 主对角线上元素都是 1,其余元素均为零的方阵称为单位矩阵,记为 \(\boldsymbol{E}\) (或\(\boldsymbol{I}\)),即\[\boldsymbol{E} = \left\lbrack \begin{matrix} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & 1 \end{matrix}\right\rbrack\](2)对角矩阵 主对角线上元素为任意常数, 而主对角线外的元素均为零的矩阵. 若对角矩阵的主对角线上的元素相等, 则称为数量矩阵
(3)三角矩阵 主对角线下方元素全为零的方阵称为上三角矩阵;主对角线上方元素全为零的方阵称为下三角矩阵; 上、下三角矩阵统称为三角矩阵
(4)对称矩阵 如果 \(n\) 阶方阵 \(\boldsymbol{A} = \left( {a}_{ij}\right)\) 满足 \({a}_{ij} = {a}_{ji}\left( {i,j = 1,2,\cdots ,n}\right)\) ,即 \({\boldsymbol{A}}^{T} = \boldsymbol{A}\) ,则称 \(\boldsymbol{A}\) 为对称矩阵
(5)反对称矩阵 如果 \(n\) 阶方阵 \(\boldsymbol{A} = \left( {a}_{ij}\right)\) 满足 \({a}_{ij} = - {a}_{ji}\left( {i \neq j}\right) ,{a}_{ii} = 0\left( {i,j = 1,2,\cdots ,n}\right)\) ,即 \({\boldsymbol{A}}^{T} = - \boldsymbol{A}\) ,则称 \(\boldsymbol{A}\) 为反对称矩阵
(6)正交矩阵 对方阵 \(\boldsymbol{A}\) ,如果有 \({\boldsymbol{A}}^{T}\boldsymbol{A} = \boldsymbol{A}{\boldsymbol{A}}^{T} = \boldsymbol{E}\) ,则称 \(\boldsymbol{A}\) 为正交矩阵
(7)幂零矩阵 对方阵 \(\boldsymbol{A}\) ,如果存在正整数 \(m\) ,使 \({\boldsymbol{A}}^{m} = \boldsymbol{0}\) ,则称 \(\boldsymbol{A}\) 为幂零矩阵
(8)幂等矩阵 满足 \({\boldsymbol{A}}^{2} = \boldsymbol{A}\) 的方阵 \(\boldsymbol{A}\) 称为幂等矩阵
(9)对合矩阵 满足 \({\boldsymbol{A}}^{2} = \boldsymbol{E}\) 的方阵 \(\boldsymbol{A}\) 称为对合矩阵
2. 逆矩阵
1. 逆矩阵的定义
对于 \(n\) 阶方阵 \(\boldsymbol{A}\) ,如果存在 \(n\) 阶方阵 \(\boldsymbol{B}\) 使 \(\boldsymbol{{AB}} = \boldsymbol{{BA}} = \boldsymbol{E}\) ,则称 \(\boldsymbol{A}\) 是可逆的, 并把 \(\boldsymbol{B}\) 称为 \(\boldsymbol{A}\) 的逆矩阵,记作 \({\boldsymbol{A}}^{-1} = \boldsymbol{B}\)
2. 关于逆矩阵的常用结论
(1)方阵 \(\boldsymbol{A}\) 可逆的充要条件是 \(\left| \boldsymbol{A}\right| \neq 0\)
(2)若 \(\boldsymbol{{AB}} = \boldsymbol{E}\) 或 \(\boldsymbol{{BA}} = \boldsymbol{E}\) ,则 \(\boldsymbol{B} = {\boldsymbol{A}}^{-1}\)
(3) \({\left( {\boldsymbol{A}}^{-1}\right) }^{-1} = \boldsymbol{A}\)
(4) \({\left( k\boldsymbol{A}\right) }^{-1} = \frac{1}{k}{\boldsymbol{A}}^{-1}\) 其中 \(k \neq 0\)
(5) \({\left( {\boldsymbol{A}}^{T}\right) }^{-1} = {\left( {\boldsymbol{A}}^{-1}\right) }^{T}\)
(6) \({\left( \boldsymbol{{AB}}\right) }^{-1} = {\boldsymbol{B}}^{-1}{\boldsymbol{A}}^{-1}\)
(7) \(\left| {\boldsymbol{A}}^{-1}\right| = {\left| \boldsymbol{A}\right| }^{-1}\)
(8)一般情况下, \({\left( \boldsymbol{A} + \boldsymbol{B}\right) }^{-1} \neq {\boldsymbol{A}}^{-1} + {\boldsymbol{B}}^{-1}\)
(9)可逆的上(下)三角矩阵的逆矩阵仍为上(下)三角矩阵
3. 伴随矩阵的定义
设 \(\boldsymbol{A} = \left( {a}_{ij}\right)\) 是 \(n\) 阶方阵,行列式 \(\left| \boldsymbol{A}\right|\) 的各个元素 \({a}_{ij}\) 的代数余子式所构成的如下的矩阵\[{\boldsymbol{A}}^{ * } = \left\lbrack \begin{matrix} {A}_{11} & {A}_{21} & \cdots & {A}_{n1} \\ {A}_{12} & {A}_{22} & \cdots & {A}_{n2} \\ \cdots & \cdots & \cdots & \cdots \\ {A}_{1n} & {A}_{2n} & \cdots & {A}_{nn} \end{matrix}\right\rbrack\]称为 \(\boldsymbol{A}\) 的伴随矩阵
4. 关于伴随矩阵的常用结论
(1)\(\boldsymbol{A}{\boldsymbol{A}}^{ * } = {\boldsymbol{A}}^{ * }\boldsymbol{A} = \left| \boldsymbol{A}\right| \boldsymbol{E}\)
(2)若 \(\boldsymbol{A}\) 可逆,则 \(\displaystyle {\boldsymbol{A}}^{-1} = \frac{1}{\left| \boldsymbol{A}\right| }{\boldsymbol{A}}^{ * },{\boldsymbol{A}}^{ * } = \left| \boldsymbol{A}\right| {\boldsymbol{A}}^{-1}\) ,且 \({\boldsymbol{A}}^{ * }\) 也可逆, \(\displaystyle {\left( {\boldsymbol{A}}^{ * }\right) }^{-1} = {\left( {\boldsymbol{A}}^{-1}\right) }^{ * } = \frac{1}{\left| \boldsymbol{A}\right| }\boldsymbol{A}\)
(3)\({\left( \boldsymbol{{AB}}\right) }^{ * } = {\boldsymbol{B}}^{ * }{\boldsymbol{A}}^{ * }\)
(4) \({\left( {\boldsymbol{A}}^{ * }\right) }^{T} = {\left( {\boldsymbol{A}}^{T}\right) }^{ * }\)
(5) \({\left( k\boldsymbol{A}\right) }^{ * } = {k}^{n - 1}{\boldsymbol{A}}^{ * }\left( {k \neq 0}\right)\)
(6) \(\left| {\boldsymbol{A}}^{ * }\right| = {\left| \boldsymbol{A}\right| }^{n - 1}\left( {n \geq 2}\right)\)
(7)\({\left( {\boldsymbol{A}}^{ * }\right) }^{ * } = {\left| \boldsymbol{A}\right| }^{n - 2}\boldsymbol{A}\left( {n \geq 2}\right)\)
3. 初等变换
1. 矩阵的初等变换
矩阵的初等行变换与初等列变换统称为初等变换. 下列三种关于矩阵的变换称为矩阵的初等行 (列) 变换:
(1)互换矩阵中两行(列)的位置 \(\left( {{r}_{i} \leftrightarrow {r}_{j},{c}_{i} \leftrightarrow {c}_{j}}\right)\)
(2)以一非零常数乘矩阵的某一行(列) \(\left( {k{r}_{i},k{c}_{j}}\right)\)
(3)将矩阵的某一行(列)的 \(k\) 倍加到另一行(列)上去 \(\left( {{r}_{i} + k{r}_{j},{c}_{i} + k{c}_{j}}\right)\)
2. 初等矩阵
(1)定义:由单位阵 \(\boldsymbol{E}\) 经过一次初等变换得到的矩阵称为初等矩阵
(2)三种初等变换对应三种初等矩阵:
①互换两行或两列的位置

②以数 \(k \neq 0\) 乘某行或某列
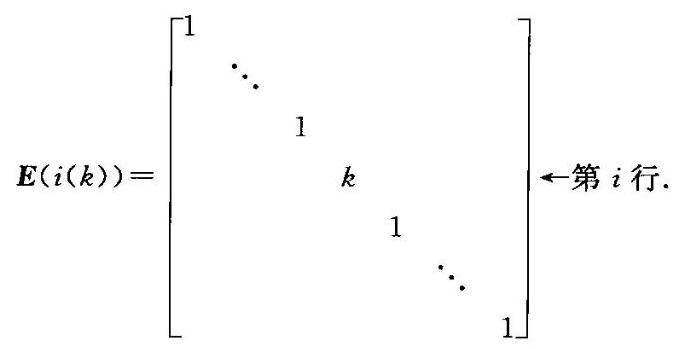
③以数 \(k\) 乘某行(列)加到另一行(列)上去

(3)
\({\boldsymbol{E}}^{T}\left( {i,j}\right) = \boldsymbol{E}\left( {i,j}\right)\)
\({\boldsymbol{E}}^{T}\left( {i\left( k\right) }\right) = \boldsymbol{E}\left( {i\left( k\right) }\right)\)
\({\boldsymbol{E}}^{T}\left( {i,j\left( k\right) }\right) = \boldsymbol{E}\left( {j,i\left( k\right) }\right)\)
\(\boldsymbol{E}^{-1}(i,j)=\boldsymbol{E}(i,j)\)
\(\boldsymbol{E}^{-1}(i(k))=\boldsymbol{E}(i(\frac1k))\)
\(\boldsymbol{E}^{-1}(i,j(k))=\boldsymbol{E}(i,j(-k))\)
\(\left| {\boldsymbol{E}\left( {i,j}\right) }\right| = - 1\)
\(\left| {\boldsymbol{E}\left( {i,j\left( k\right) }\right) }\right| = 1\)
3. 初等变换与初等矩阵的联系
设 \(\boldsymbol{A}\) 是 \(m \times n\) 矩阵,对 \(\boldsymbol{A}\) 施行一次初等行变换,相当于在 \(\boldsymbol{A}\) 的左边乘以相应的 \(m\) 阶初等矩阵; 对 \(\boldsymbol{A}\) 施行一次初等列变换,相当于在 \(\boldsymbol{A}\) 的右边乘以相应的 \(n\) 阶初等矩阵
4. 初等变换化简矩阵
(1)行阶梯形矩阵: 可画出一条阶梯线,线的下方全为 0,每个台阶只有一行,台阶数即是非零行的行数, 阶梯线的竖线后面的第一个元素为非零元, 就是非零行的第一个非零元
(2)行最简形矩阵: 非零行的第一个非零元为 1 ,且这些非零元所在的列的其他元素都为 0
(3)对于任何矩阵 \(\boldsymbol{A}\) ,总可经过有限次初等行变换把它变为行阶梯形矩阵和行最简形矩阵
(4) 标准型: 对于 \(m \times n\) 矩阵 \(\boldsymbol{A}\) ,总可经过初等变换,把它化为 \(\boldsymbol{F} = {\left\lbrack \begin{matrix} {\boldsymbol{E}}_{r} & \boldsymbol{0} \\ \boldsymbol{0} & {\boldsymbol{0}} \end{matrix}\right\rbrack }_{m \times n}\) 称为等价标准型
5. 矩阵等价
(1)矩阵 \(\boldsymbol{A}\) 经过一系列的初等变换得到矩阵 \(\boldsymbol{B}\) ,则称 \(\boldsymbol{A},\boldsymbol{B}\) 等价. 特别地, \(\boldsymbol{A}\) 经过一系列初等行 (列) 变换得到 \(\boldsymbol{B}\) ,称 \(\boldsymbol{A},\boldsymbol{B}\) 行 (列) 等价
(2)方阵 \(\boldsymbol{A}\) 可逆的充要条件是存在有限个初等矩阵 \({\boldsymbol{P}}_{1},{\boldsymbol{P}}_{2},\cdots ,{\boldsymbol{P}}_{t}\) ,使 \(\boldsymbol{A} = {\boldsymbol{P}}_{1}\cdots {\boldsymbol{P}}_{t}\)
(3)方阵 \(\boldsymbol{A}\) 可逆的充要条件是 \(\boldsymbol{A}\) 与单位矩阵等价
(4) \(m \times n\) 矩阵 \(\boldsymbol{A}\) 和 \(\boldsymbol{B}\) 等价的充要条件是存在 \(m\) 阶可逆矩阵 \(\boldsymbol{P}\) 和 \(n\) 阶可逆矩阵 \(\boldsymbol{Q}\) ,使 \(\boldsymbol{{PAQ}} =\)B
(5) \(m \times n\) 矩阵 \(\boldsymbol{A}\) 和 \(\boldsymbol{B}\) 等价的充要条件是 \(\boldsymbol{A}\) 和 \(\boldsymbol{B}\) 有相同的秩
6. 初等变换求逆矩阵
(1) \(\left( {\boldsymbol{A}\,\cdots \, \boldsymbol{E}}\right) \xrightarrow[]{\text{ 初等行变换 }}\left( {\boldsymbol{E}\,\cdots\, {\boldsymbol{A}}^{-1}}\right)\)
(2) \(\left\lbrack \begin{array}{l} \boldsymbol{A} \\ \cdots \\ \boldsymbol{E} \end{array}\right\rbrack\) 初等列变换, \(\left\lbrack \begin{matrix} \boldsymbol{E} \\ \cdots \\ {\boldsymbol{A}}^{-1} \end{matrix}\right\rbrack\)
(3) \(\left\lbrack \begin{array}{ll} \boldsymbol{A} & \boldsymbol{E} \\ \boldsymbol{E} & \boldsymbol{0} \end{array}\right\rbrack \xrightarrow[]{\text{ 初等行,列变换 }}\left\lbrack \begin{array}{ll} \boldsymbol{E} & \boldsymbol{C} \\ \boldsymbol{B} & \boldsymbol{0} \end{array}\right\rbrack\) ,则 \({\boldsymbol{A}}^{-1} = \boldsymbol{{BC}}\)
7. 初等矩阵的推广
(1) 设 \({\boldsymbol{A}}_{m \times n} = {\left( {a}_{ij}\right) }_{m \times n},\;{\boldsymbol{E}}_{ij} = \left\lbrack \begin{matrix} 0 & & \cdots & & &\\ & \ddots & \cdots & & & \\ \cdots & \cdots & 1 & \cdots & \cdots & \cdots \\ & & \cdots & 0 & & \\ & & \cdots & & \ddots & \\ & & \cdots & & & 0 \end{matrix}\right\rbrack\) ,则\[{\boldsymbol{E}}_{ij}\boldsymbol{A} = \left\lbrack \begin{matrix} 0 & & & & & & \\ & 0 & & & & & \\ & & \ddots & & & & \\ & & & 1 & & & \\ & & & & 0 & & \\ & & & & & \ddots & \\ & & & & & & 0 \end{matrix}\right\rbrack \boldsymbol{A} = \left\lbrack \begin{matrix} 0 & 0 & \cdots & 0 \\ \cdots & \cdots & & \cdots \\ {a}_{j1} & {a}_{j2} & \cdots & {a}_{jn} \\ 0 & 0 & \cdots & 0 \\ \cdots & \cdots & & \cdots \\ 0 & 0 & \cdots & 0 \end{matrix}\right\rbrack\]即 \(\boldsymbol{A}\) 左乘 \({\boldsymbol{E}}_{ij}\) 相当于把 \(\boldsymbol{A}\) 中第 \(i\) 行换成第 \(j\) 行元素,其他元素为 0 . 类似地,\[\boldsymbol{A}{\boldsymbol{E}}_{ij} = \boldsymbol{A}\left\lbrack \begin{array}{lllllll} 0 & & & & & & \\ & 0 & & & & & \\ & & \ddots & & & & \\ & & & 1 & & & \\ & & & & 0 & & \\ & & & & & \ddots & \\ & & & & & & 0 \end{array}\right\rbrack = \left\lbrack \begin{matrix} 0 & \cdots & 0 & {a}_{1i} & 0 & \cdots & 0 \\ 0 & \cdots & 0 & {a}_{2i} & 0 & \cdots & 0 \\ \cdots & & \cdots & \cdots & \cdots & & \\ 0 & \cdots & 0 & {a}_{ni} & 0 & \cdots & 0 \end{matrix}\right\rbrack\]即 \(\boldsymbol{A}\) 右乘 \({\boldsymbol{E}}_{ij}\) 相当于把 \(\boldsymbol{A}\) 中第 \(j\) 列换成第 \(i\) 列元素,其他元素都为 0
(2)设 \(\boldsymbol{A} = \left\lbrack \begin{matrix} {\boldsymbol{\alpha }}_{1} \\ \cdots \\ {\boldsymbol{\alpha }}_{n} \end{matrix}\right\rbrack\) ,其中 \({\boldsymbol{\alpha }}_{i}\) 为 \(\boldsymbol{A}\) 的行向量, \(i = 1,\cdots ,n\) ,则\[\left\lbrack \begin{array}{llll} & & & 1 \\ & & 1 & \\ & {\Large ⋰} & & \\ 1 & & & \end{array}\right\rbrack \boldsymbol{A} = \left\lbrack \begin{array}{llll} & & & 1 \\ & & 1 & \\ & {\Large ⋰} & & \\ & & & \end{array}\right\rbrack \left\lbrack \begin{matrix} {\boldsymbol{\alpha }}_{1} \\ \cdots \\ {\boldsymbol{\alpha }}_{n} \end{matrix}\right\rbrack = \left\lbrack \begin{matrix} {\boldsymbol{\alpha }}_{n} \\ \cdots \\ {\boldsymbol{\alpha }}_{1} \end{matrix}\right\rbrack\]即 \(\boldsymbol{A}\) 左乘 \(\left\lbrack \begin{array}{llll} & & & 1 \\ & & 1 & \\ & {\Large ⋰} & & \\ 1 & & & \end{array}\right\rbrack\) 相当于把矩阵 \(\boldsymbol{A}\) 的行向量颠倒了一下
同理设 \(\boldsymbol{A} = \left( {{\boldsymbol{\beta }}_{1},\cdots ,{\boldsymbol{\beta }}_{n}}\right)\) ,其中 \({\boldsymbol{\beta }}_{j}\) 为 \(\boldsymbol{A}\) 的列向量, \(j = 1,\cdots ,n\) ,则\[\boldsymbol{A}\left\lbrack \begin{array}{llll} & & & 1 \\ & & 1 & \\ & {\Large ⋰} & & \\ 1 & & & \end{array}\right\rbrack = \left( {{\boldsymbol{\beta }}_{1},\cdots ,{\boldsymbol{\beta }}_{n}}\right) \left\lbrack \begin{array}{llll} & & & 1 \\ & & 1 & \\ & {\Large ⋰} & & \\ 1 & & & \end{array}\right\rbrack = \left( {{\boldsymbol{\beta }}_{n},\cdots ,{\boldsymbol{\beta }}_{1}}\right)\]即 \(\boldsymbol{A}\) 右乘 \(\left\lbrack \begin{array}{llll} & & & 1 \\ & & 1 & \\ & {\Large ⋰} & & \\ 1 & & & \end{array}\right\rbrack\) 相当于把矩阵 \(\boldsymbol{A}\) 的列向量颠倒了一下
(3) 设 \(\boldsymbol{A} = \left\lbrack \begin{matrix} {\boldsymbol{\alpha }}_{1} \\ \cdots \\ {\boldsymbol{\alpha }}_{n} \end{matrix}\right\rbrack\) ,其中 \({\boldsymbol{\alpha }}_{i}\) 为 \(\boldsymbol{A}\) 的行向量, \(i = 1,\cdots ,n\) ,则\[\left\lbrack \begin{matrix} 0 & 1 & & \\ & 0 & \ddots & \\ & & \ddots & 1 \\ & & & 0 \end{matrix}\right\rbrack \boldsymbol{A} = \left\lbrack \begin{matrix} 0 & 1 & & \\ & 0 & \ddots & \\ & & \ddots & 1 \\ & & & 0 \end{matrix}\right\rbrack \left\lbrack \begin{matrix} {\boldsymbol{\alpha }}_{1} \\ \cdots \\ {\boldsymbol{\alpha }}_{n} \end{matrix}\right\rbrack = \left\lbrack \begin{matrix} {\boldsymbol{\alpha }}_{2} \\ \cdots \\ {\boldsymbol{\alpha }}_{n} \\ \boldsymbol{0} \end{matrix}\right\rbrack\]即矩阵 \(\boldsymbol{A}\) 左乘 \(\left\lbrack \begin{array}{llll} 0 & 1 & & \\ & \ddots & \ddots & \\ & & \ddots & 1 \\ & & & 0 \end{array}\right\rbrack\) 相当于把 \(\boldsymbol{A}\) 的各行向上递推了一次. 类似地,\[\left\lbrack \begin{matrix} 0 & & & \\ 1 & \ddots & & \\ & \ddots & \ddots & \\ & & \ddots & 0 \\ & & & 1 \end{matrix}\right\rbrack \boldsymbol{A} = \left\lbrack \begin{matrix} 0 & & & \\ 1 & \ddots & & \\ & \ddots & \ddots & \\ & & \ddots & 0 \\ & & & 1 \end{matrix}\right\rbrack \left\lbrack \begin{matrix} {\boldsymbol{\alpha }}_{1} \\ \cdots \\ {\boldsymbol{\alpha }}_{n} \end{matrix}\right\rbrack = \left\lbrack \begin{matrix} \boldsymbol{0} \\ {\boldsymbol{\alpha }}_{1} \\ \cdots \\ {\boldsymbol{\alpha }}_{n - 1} \end{matrix}\right\rbrack\]即矩阵 \(\boldsymbol{A}\) 左乘 \(\left\lbrack \begin{array}{llll} 0 & & & \\ 1 & \ddots & & \\ & \ddots & \ddots & \\ & & \ddots & 0 \\ & & & 1 \end{array}\right\rbrack\) 相当于把 \(\boldsymbol{A}\) 的各行向下递推了一次
同理设 \(\boldsymbol{A} = \left( {{\boldsymbol{\beta }}_{1},\cdots ,{\boldsymbol{\beta }}_{n}}\right)\) ,其中 \({\boldsymbol{\beta }}_{j}\) 为 \(\boldsymbol{A}\) 的列向量, \(j = 1,2,\cdots ,n\) ,则\[\boldsymbol{A}\left\lbrack \begin{array}{llll} 0 & 1 & & \\ & \ddots & \ddots & \\ & & \ddots & 1 \\ & & & 0 \end{array}\right\rbrack = \left( {{\boldsymbol{\beta }}_{1},\cdots ,{\boldsymbol{\beta }}_{n}}\right) \left\lbrack \begin{array}{llll} 0 & 1 & & \\ & \ddots & \ddots & \\ & & \ddots & 1 \\ & & & 0 \end{array}\right\rbrack = \left( {\boldsymbol{0},{\boldsymbol{\beta }}_{1},\cdots ,{\boldsymbol{\beta }}_{n - 1}}\right)\]即矩阵 \(\boldsymbol{A}\) 右乘 \(\left\lbrack \begin{array}{llll} 0 & 1 & & \\ & \ddots & \ddots & \\ & & \ddots & 1 \\ & & & 0 \end{array}\right\rbrack\) 相当于把 \(\boldsymbol{A}\) 的列向量向右递推一次. 类似地,\[\boldsymbol{A}\left\lbrack \begin{array}{llll} 0 & & & \\ 1 & \ddots & & \\ & \ddots & \ddots & \\ & & 1 & 0 \end{array}\right\rbrack = \left( {{\boldsymbol{\beta }}_{1},\cdots ,{\boldsymbol{\beta }}_{n}}\right) \left\lbrack \begin{array}{llll} 0 & & & \\ 1 & \ddots & & \\ & \ddots & \ddots & \\ & & 1 & 0 \end{array}\right\rbrack = \left( {{\boldsymbol{\beta }}_{2},\cdots ,{\boldsymbol{\beta }}_{n},\boldsymbol{0}}\right)\]即矩阵 \(\boldsymbol{A}\) 右乘 \(\left\lbrack \begin{array}{llll} 0 & & & \\ 1 & \ddots & & \\ & \ddots & \ddots & \\ & & 1 & 0 \end{array}\right\rbrack\) 相当于把 \(\boldsymbol{A}\) 的列向量向左递推一次
4. 矩阵的秩
1. \(k\) 阶子式
在 \(m \times n\) 矩阵 \(\boldsymbol{A}\) 中,任取 \(k\) 行 \(k\) 列,则其交叉处的 \({k}^{2}\) 个元素按原顺序组成一个 \(k\) 阶矩阵,其行列式称为 \(\boldsymbol{A}\) 的一个 \(k\) 阶子式
2. 矩阵的秩 矩阵 \(\boldsymbol{A}\) 的不为零的子式的最高阶数称为 \(\boldsymbol{A}\) 的秩,记为 \(r\left( \boldsymbol{A}\right)\)
3. 常用公式和结论
设 \(\boldsymbol{A}\) 为 \(m \times n\) 矩阵, \(\boldsymbol{B}\) 为 \(n \times l\) 矩阵,则
(1)\( 0 \leq r\left( \boldsymbol{A}\right) \leq \min \{ m,n\}\)
(2)\(r\left( {\boldsymbol{A}}^{T}\right) = r\left( \boldsymbol{A}\right)\)
(3)若 \(\boldsymbol{A} \neq \boldsymbol{0}\) ,则 \(r\left( \boldsymbol{A}\right) \geq 1\)
(4) \(r\left( {\boldsymbol{A} \pm \boldsymbol{B}}\right) \leq r\left( \boldsymbol{A}\right) + r\left( \boldsymbol{B}\right)\)
(5)若 \(\boldsymbol{P}\) 可逆,则 \(r\left( {\boldsymbol{P}\boldsymbol{A}}\right) = r\left( \boldsymbol{A}\right)\) ; 若 \(\boldsymbol{Q}\) 可逆,则 \(r\left( \boldsymbol{{AQ}}\right) = r\left( \boldsymbol{A}\right)\)
(6) \(r\left( \boldsymbol{{AB}}\right) \leq \min \{ r\left( \boldsymbol{A}\right) ,r\left( \boldsymbol{B}\right) \}\)
(7) \(r\left( \boldsymbol{{AB}}\right) \geq r\left( \boldsymbol{A}\right) + r\left( \boldsymbol{B}\right) - n\)
(8)若 \(\boldsymbol{{AB}} = \boldsymbol{0}\) ,则 \(r\left( \boldsymbol{A}\right) + r\left( \boldsymbol{B}\right) \leq n\)
(9)\(\boldsymbol{A}\) 行满秩 \(\Leftrightarrow r\left( \boldsymbol{A}\right) = m \Leftrightarrow \boldsymbol{A}\) 的等价标准型为 \(\left( \begin{array}{ll} {\boldsymbol{E}}_{m} & \boldsymbol{0} \end{array}\right)\)
(10)\(\boldsymbol{A}\) 列满秩 \(\Leftrightarrow r\left( \boldsymbol{A}\right) = n \Leftrightarrow \boldsymbol{A}\) 的等价标准型为 \(\left\lbrack \begin{matrix} {\boldsymbol{E}}_{n} \\ \boldsymbol{0} \end{matrix}\right\rbrack\)
(11)若 \(\boldsymbol{A}\) 是 \(n\) 阶方阵,则 \(r\left( \boldsymbol{A}\right) = n \Leftrightarrow \left| \boldsymbol{A}\right| \neq 0,r\left( \boldsymbol{A}\right) < n \Leftrightarrow \left| \boldsymbol{A}\right| = 0\)
(12)同型矩阵 \(\boldsymbol{A}\text{ 、 }\boldsymbol{B}\) 等价的充要条件是 \(r\left( \boldsymbol{A}\right) = r\left( \boldsymbol{B}\right)\)
(13)设 \({\boldsymbol{A}}^{ * }\) 是 \(n\) 阶方阵 \(\boldsymbol{A}\) 的伴随矩阵,则\[r\left( {\boldsymbol{A}}^{ * }\right) = \left\{ \begin{array}{ll} n & \text{ 若 }r\left( \boldsymbol{A}\right) = n, \\ 1 & \text{ 若 }r\left( \boldsymbol{A}\right) = n - 1, \\ 0 & \text{ 若 }r\left( \boldsymbol{A}\right) < n - 1. \end{array}\right.\]
5. 分块矩阵
1. 分块矩阵的定义
将矩阵 \(\boldsymbol{A}\) 用若干条纵线和横线分成许多个小矩阵,每个小矩阵称为 \(\boldsymbol{A}\) 的子块,以子块为元素的形式上的矩阵称为分块矩阵.
如: \(\boldsymbol{A} = \left\lbrack \begin{matrix} {a}_{11} & {a}_{12} & {a}_{13} \\ {a}_{21} & {a}_{22} & {a}_{23} \\ {a}_{31} & {a}_{32} & {a}_{33} \end{matrix}\right\rbrack = \left\lbrack \begin{array}{l} {\boldsymbol{\alpha }}_{1} \\ {\boldsymbol{\alpha }}_{2} \\ {\boldsymbol{\alpha }}_{3} \end{array}\right\rbrack\)
其中 \({\boldsymbol{\alpha }}_{1} = \left( {{a}_{11},{a}_{12},{a}_{13}}\right)\) 是一个子块
又如: \(\;\boldsymbol{B} = \left\lbrack \begin{array}{llll} {b}_{11} & {b}_{12} & {b}_{13} & {b}_{14} \\ {b}_{21} & {b}_{22} & {b}_{23} & {b}_{24} \\ {b}_{31} & {b}_{32} & {b}_{33} & {b}_{34} \\ {b}_{41} & {b}_{42} & {b}_{43} & {b}_{44} \end{array}\right\rbrack = \left\lbrack \begin{array}{ll} {\boldsymbol{B}}_{1} & {\boldsymbol{B}}_{2} \\ {\boldsymbol{B}}_{3} & {\boldsymbol{B}}_{4} \end{array}\right\rbrack\)
其中 \({\boldsymbol{B}}_{1} = \left\lbrack \begin{array}{ll} {b}_{11} & {b}_{12} \\ {b}_{21} & {b}_{22} \end{array}\right\rbrack ,{\boldsymbol{B}}_{2} = \left\lbrack \begin{array}{ll} {b}_{13} & {b}_{14} \\ {b}_{23} & {b}_{24} \end{array}\right\rbrack ,{\boldsymbol{B}}_{3} = \left\lbrack \begin{array}{ll} {b}_{31} & {b}_{32} \\ {b}_{41} & {b}_{42} \end{array}\right\rbrack ,{\boldsymbol{B}}_{4} = \left\lbrack \begin{array}{ll} {b}_{33} & {b}_{34} \\ {b}_{43} & {b}_{44} \end{array}\right\rbrack\) , 则 \({\boldsymbol{B}}_{1},{\boldsymbol{B}}_{2},{\boldsymbol{B}}_{3},{\boldsymbol{B}}_{4}\) 是 \(\boldsymbol{B}\) 的子块
同一矩阵分成子块的分法有很多
2. 分块矩阵的运算
(1)分块矩阵的加减法 若矩阵 \(\boldsymbol{A}\) 与矩阵 \(\boldsymbol{B}\) 有相同的行数和列数,且有\[\boldsymbol{A} = \left\lbrack \begin{matrix} {\boldsymbol{A}}_{11} & \cdots & {\boldsymbol{A}}_{1r} \\ \cdots & & \cdots \\ {\boldsymbol{A}}_{s1} & \cdots & {\boldsymbol{A}}_{sr} \end{matrix}\right\rbrack ,\;\boldsymbol{B} = \left\lbrack \begin{matrix} {\boldsymbol{B}}_{11} & \cdots & {\boldsymbol{B}}_{1r} \\ \cdots & & \cdots \\ {\boldsymbol{B}}_{s1} & \cdots & {\boldsymbol{B}}_{sr} \end{matrix}\right\rbrack\]其中 \({\boldsymbol{A}}_{ij}\) 与 \({\boldsymbol{B}}_{ij}\) 有相同的行数和列数,则\[\boldsymbol{A} \pm \boldsymbol{B} = \left\lbrack \begin{matrix} {\boldsymbol{A}}_{11} \pm {\boldsymbol{B}}_{11} & \cdots & {\boldsymbol{A}}_{1r} \pm {\boldsymbol{B}}_{1r} \\ \cdots & & \cdots \\ {\boldsymbol{A}}_{s1} \pm {\boldsymbol{B}}_{s1} & \cdots & {\boldsymbol{A}}_{sr} \pm {\boldsymbol{B}}_{sr} \end{matrix}\right\rbrack \](2)分块矩阵的数乘 设矩阵 \(\boldsymbol{A} = \left\lbrack \begin{matrix} {\boldsymbol{A}}_{11} & \cdots & {\boldsymbol{A}}_{1r} \\ \cdots & & \cdots \\ {\boldsymbol{A}}_{s1} & \cdots & {\boldsymbol{A}}_{sr} \end{matrix}\right\rbrack ,\lambda\) 为数,则\[\lambda \boldsymbol{A} = \left\lbrack \begin{matrix} \lambda {\boldsymbol{A}}_{11} & \cdots & \lambda {\boldsymbol{A}}_{1r} \\ \cdots & & \cdots \\ \lambda {\boldsymbol{A}}_{s1} & \cdots & \lambda {\boldsymbol{A}}_{sr} \end{matrix}\right\rbrack\](3)分块矩阵的乘法 若 \(\boldsymbol{A}\) 为 \(m \times l\) 矩阵, \(\boldsymbol{B}\) 为 \(l \times n\) 矩阵,且\[\boldsymbol{A} = \left\lbrack \begin{matrix} {\boldsymbol{A}}_{11} & \cdots & {\boldsymbol{A}}_{1t} \\ \cdots & & \cdots \\ {\boldsymbol{A}}_{s1} & \cdots & {\boldsymbol{A}}_{st} \end{matrix}\right\rbrack ,\;\boldsymbol{B} = \left\lbrack \begin{matrix} {\boldsymbol{B}}_{11} & \cdots & {\boldsymbol{B}}_{1r} \\ \cdots & & \cdots \\ {\boldsymbol{B}}_{t1} & \cdots & {\boldsymbol{B}}_{tr} \end{matrix}\right\rbrack\]其中 \({\boldsymbol{A}}_{i1},{\boldsymbol{A}}_{i2},\cdots ,{\boldsymbol{A}}_{it}\) 的列数分别与 \({\boldsymbol{B}}_{1j},{\boldsymbol{B}}_{2j},\cdots ,{\boldsymbol{B}}_{tj}\) 的行数相等,则\[\boldsymbol{{AB}} = \left\lbrack \begin{matrix} {\boldsymbol{C}}_{11} & \cdots & {\boldsymbol{C}}_{1r} \\ \cdots & & \cdots \\ {\boldsymbol{C}}_{s1} & \cdots & {\boldsymbol{C}}_{rr} \end{matrix}\right\rbrack\]其中 \({\boldsymbol{C}}_{ij} = \mathop{\sum }\limits_{{k = 1}}^{l}{\boldsymbol{A}}_{ik}{\boldsymbol{B}}_{kj}\;\left( {i = 1,\cdots ,s;\; j = 1,\cdots ,r}\right)\)
(4)分块矩阵的转置 设矩阵 \(\boldsymbol{A} = \left\lbrack \begin{matrix} {\boldsymbol{A}}_{11} & \cdots & {\boldsymbol{A}}_{1r} \\ \cdots & & \cdots \\ {\boldsymbol{A}}_{s1} & \cdots & {\boldsymbol{A}}_{sr} \end{matrix}\right\rbrack\) ,则 \({\boldsymbol{A}}^{T} = \left\lbrack \begin{matrix} {\boldsymbol{A}}_{11}^{T} & \cdots & {\boldsymbol{A}}_{s1}^{T} \\ \cdots & & \cdots \\ {\boldsymbol{A}}_{1r}^{T} & \cdots & {\boldsymbol{A}}_{sr}^{T} \end{matrix}\right\rbrack\)
3. 分块矩阵常用结论
(1)设 \(\boldsymbol{A} = \left\lbrack \begin{array}{llll} {\boldsymbol{A}}_{1} & & & \\ & {\boldsymbol{A}}_{2} & & \\ & & \ddots & \\ & & & {\boldsymbol{A}}_{m} \end{array}\right\rbrack\) ,其中 \({\boldsymbol{A}}_{i}\left( {i = 1,2,\cdots ,m}\right)\) 都是方阵,则\[\left| \boldsymbol{A}\right| = \left| {\boldsymbol{A}}_{1}\right| \cdots \left| {\boldsymbol{A}}_{m}\right| ,\;{\boldsymbol{A}}^{n} = \left\lbrack \begin{array}{llll} {\boldsymbol{A}}_{1}^{n} & & & \\ & {\boldsymbol{A}}_{2}^{n} & & \\ & & \ddots & \\ & & & {\boldsymbol{A}}_{m}^{n} \end{array}\right\rbrack\](2) 设 \(\boldsymbol{A} = \left\lbrack \begin{array}{llll} {\boldsymbol{A}}_{1} & & & \\ & {\boldsymbol{A}}_{2} & & \\ & & \ddots & \\ & & & {\boldsymbol{A}}_{m} \end{array}\right\rbrack ,{\boldsymbol{A}}_{i}\left( {i = 1,2,\cdots ,m}\right)\) 均为可逆矩阵,则\[{\boldsymbol{A}}^{-1} = \left\lbrack \begin{array}{llll} {\boldsymbol{A}}_{1}^{-1} & & & \\ & {\boldsymbol{A}}_{2}^{-1} & & \\ & & \ddots & \\ & & & {\boldsymbol{A}}_{m}^{-1} \end{array}\right\rbrack\](3) 设 \(\boldsymbol{A} = \left\lbrack \begin{array}{llll} & & & {\boldsymbol{A}}_{1} \\ & & {\boldsymbol{A}}_{2} & \\ & {\Large ⋰} & & \\ {\boldsymbol{A}}_{m} & & & \end{array}\right\rbrack ,{\boldsymbol{A}}_{i}\left( {i = 1,\cdots ,m}\right)\) 均为可逆矩阵,则\[{\boldsymbol{A}}^{-1} = \left\lbrack \begin{matrix} & & & {\boldsymbol{A}}_{m}^{-1} \\ & & {\Large ⋰} & \\ & {\boldsymbol{A}}_{2}^{-1} & & \\ {\boldsymbol{A}}_{1}^{-1} & & & \end{matrix}\right\rbrack\](4)设 \(\boldsymbol{A},\boldsymbol{B}\) 为方阵,则 \(\left| \begin{matrix} \boldsymbol{A} & \boldsymbol{C} \\ \boldsymbol{0} & \boldsymbol{B} \end{matrix}\right| = \left| \begin{matrix} \boldsymbol{A} & \boldsymbol{0} \\ \boldsymbol{0} & \boldsymbol{B} \end{matrix}\right| = \left| \begin{matrix} \boldsymbol{A} & \boldsymbol{0} \\ \boldsymbol{D} & \boldsymbol{B} \end{matrix}\right| = \left| \boldsymbol{A}\right| \left| \boldsymbol{B}\right|\)
6. 矩阵方程
1.矩阵方程 \(\boldsymbol{{AX}} = \boldsymbol{B} \) 有解 \( \Leftrightarrow r\left( \boldsymbol{A}\right) = r\left( {\boldsymbol{A},\boldsymbol{B}}\right) \)
2. 求解矩阵方程 \( \boldsymbol{{AX}} = \boldsymbol{B} \Leftrightarrow \) 求解线性方程组 \( \boldsymbol{A}{\boldsymbol{x}}_{i} = {\boldsymbol{b}}_{i}\left( {i = 1,\cdots ,n}\right) \)
3.求解矩阵方程 \( \boldsymbol{X}\boldsymbol{A} = \boldsymbol{B} \Leftrightarrow \) 求解矩阵方程\( {\boldsymbol{A}}^{T}{\boldsymbol{X}}^{T} = {\boldsymbol{B}}^{T} \)
4.特别地,若 \( \boldsymbol{A} \) 可逆,则 \( \boldsymbol{{AX}} = \boldsymbol{B} \) 有唯一解 \( \boldsymbol{X} = {\boldsymbol{A}}^{-1}\boldsymbol{B},\boldsymbol{{XA}} = \boldsymbol{B} \) 有唯一解 \( \boldsymbol{X} = \boldsymbol{B}{\boldsymbol{A}}^{-1} \)
5.对于其他形式的矩阵方程可考虑待定系数法



